智能安全键盘软硬件完整方案

我们可以把-1看成一个常量输入，它的权系数theta在学习的过程中进行调整。这样，当SUM(Xi*Wi)+(-1*theta)>=0时，y=1，反之y=0。

在学习过程中，神经网络输入一系列需要分类的术语示例和它们的正确分类或者目标。

这样的输入可以看成一个向量：，这里t是一个目标或者正确分类。神经网络用这些来调整权系数，其目的使学习中的目标与其分类相匹配。更确切地说，这是有指导的学习，与之相反的是无指导的学习。前者是基于带目标的示例，而后者却只是建立在统计分析的基础上。权系数的调整有一个学习规则，一个理想化的学习算法如下所示：

fully_trained = FALSE

DO UNTIL (fully_trained):

fully_trained = TRUE

FOR EACH training_vector = ::

# Weights compared to theta

a = (X1 * W1)+(X2 * W2)+...+(Xn * Wn) - theta

y = sigma(a)

IF y != target:

fully_trained = FALSE

FOR EACH Wi:

MODIFY_WEIGHT(Wi) # According to the training rule

IF (fully_trained):

BREAK

学习规则有很多，通过对收集的大量资料的研究分析，我们发现，有一条似乎合理的规则是基于这样一种思想，即权系数和阈值的调整应该由分式(t-y)确定。这个规则通过引入学习率alpha(0

关于 delta 规则

delta 规则是基于梯度降落这样一种思路的。在权系数的调整中，神经网络将会找到一种将误差减少到最小的权系数的分配方式。

将我们的网络限制为没有隐藏节点，但是可能会有不止一个的输出节点，设p是一组学习中的一个元素，t(p,n)是相应的输出节点n的目标。设y(p,n)由以上提到的squash函数s决定，这里a(p,n)是与p相关的n的激活函数，或者用(p,n)=s(a(p,n))表示为与p相关的节点n的squash过的激活函数。为网络设定权系数(每个Wi)，也为每个p和n建立t(p,n)与y(p,n)的差分，这就意味着为每个p设定了网络全部的误差。因此对于每组权系数来说有一个平均误差。但是delta规则取决于求平均值方法的精确度以及误差。对于每个Wi，平均误差定义如下：

sum = 0

FOR p = 1 TO M: # M is number of training vectors

FOR n = 1 TO N: # N is number of output nodes

sum = sum + (1/2 * (t(p,n)-y(p,n))^2)

average = 1/M * sum

delta规则就是依据这个误差的定义来定义的。因为误差是依据那些学习向量来说明的，delta规则是一种获取一个特殊的权系数集以及一个特殊的向量的算法。而改变权系数将会使神经网络的误差最小化。任何Wi发生的变化都如下所示：alpha*s'(a(p,n))*(t(p,n)-y(p,n))*X(p,i,n)。

X(p,i,n)是输入到节点n的p中的第i个元素，alpha是已知的学习率。最后s'(a(p,n))是与p相关的第n个节点激活的squashing函数的变化(派生)率，这就是delta规则，并且当alpha非常小的时候，权系数向量接近某个将误差最小化的向量。用于权系数调节的基于delta规则的算法就是如此。

梯度降落(直到误差小到适当的程度为止)如下：

step 1: for each training vector, p, find a(p)

step 2: for each i, change Wi by:

alpha * s'(a(p,n)) * (t(p,n)-y(p,n)) * X(p,i,n)

delta规则算法总是在权系数上调整，而且这是建立在相对输出的激活方式上，不一定适用于存在隐藏节点的网络。

反向传播

反向传播这一算法把支持delta规则的分析扩展到了带有隐藏节点的神经网络。当输出节点从隐藏节点获得输入，网络发现出现了误差，权系数的调整可以通过一个算法来找出整个误差是由多少不同的节点造成的，具体方法如下：

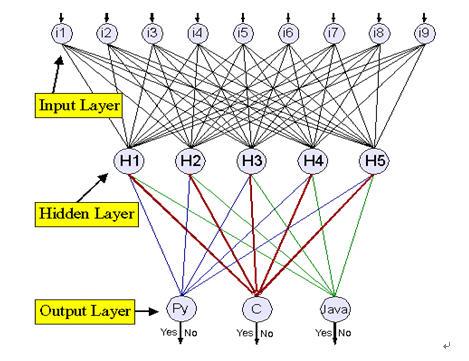
“代码识别”反向传播的神经网络

反向传播算法同样来源于梯度降落原理，在权系数调整分析中的唯一不同是涉及到t(p,n)与y(p,n)的差分。通常来说Wi的改变在于：

alpha * s'(a(p,n)) * d(n) * X(p,i,n)

其中d(n)是隐藏节点n的函数。一方面，n影响输出节点越多，n造成网络整体的误差也越多。另一方面，如果输出节点影响网络整体的误差越少，n对输出节点的影响也相应减少。这里d(j)是对网络的整体误差的基值，W(n,j)是n对j造成的影响，d(j)*W(n,j)是这两种影响的总和。但是n几乎总是影响多个输出节点，也许会影响每一个输出结点，这样，d(n)可以表示为：SUM(d(j)*W(n,j))

这里j是一个从n获得输入的输出节点，联系起来，我们就得到了一个学习规则。

第1部分：在隐藏节点n和输出节点j之间权系数改变，如下所示：

alpha * s'(a(p,n))*(t(p,n) - y(p,n)) * X(p,n,j)

第2部分：在输入节点i和输出节点n之间权系数改变，如下所示：

alpha * s'(a(p,n)) * sum(d(j) * W(n,j)) * X(p,i,n)

这里每个从n接收输入的输出节点j都