基于单接收头的超声波多目标测距机实现方案

　　超声波测距传感器以其测量精度高、响应快和价格低廉而广泛应用在工业现场测距、移动机器人导航和定位等场合。超声波测距传感器常用的方式是1 个发射头对应1 个接收头，也有多个发射头对应1 个接收头。 它们共同之处是：每个接收头只测量一个位置，这个位置就是除盲区内因发射的超声波旁瓣引起的接收信号超声波包络峰值外，第1个接收信号超声波包络峰值对应的距离。 在机器人自主导航避障时，机器人只关心最近障碍物的距离，是能够完成自主避障的。 但是在机器人定位时，尤其在动态环境下，1 个接收头同时测量多个距离，能够更多地描述环境信息，这对机器人用超声波定位具有重要意义。

1 超声波

1. 1 超声波测距原理

超声波测距原理比较简单，一般是采用时差法。即：通过检测发射的超声波与其遇到障碍物后产生回波之间的时间差Δt ，求出障碍物的距离d ，计算公式为： d = cΔt/ 2 ，其中：

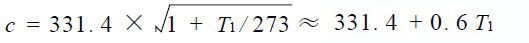
c 为超声波波速， T1 为环境摄氏温度。

1. 2 发射信号超声波包络

在发射头两端加40 kHZ 的矩形脉冲电压， 压电晶体把电能转变成机械能，带动其上振动板运动，见图1. 振动板的固有频率是40 kHZ，由于共振，振动板很快起振，然后稳定， 脉冲电压撤销， 振动板作阻尼振荡衰减。 若振动板长时间工作在最大振幅状态，即振动板新增能量与其损耗能量相等，这样产生的超声波能量大，有利于提高信噪比，但是接收信号超声波包络从起振到峰值的时间将变长（放大器增益小，不出现削顶的情况下） ，不利于阈值选择，误差变大，也不利于第二个位置的测量，另外盲区也会增大。 振动板振动时，空气、压电晶体（起振时是激励）等消耗振动板能量， 其中受空气阻力消耗的能量转变成发射超声波。 压电晶体激励撤销，则振动板振动作阻尼呈指数关系衰减。 把振动板简化成是一个弹簧振子，设振动板在一个正弦周期（ T = 25μs） 内是标准正弦波，则在发射头振动板运动周期数n ≤发射头激励脉冲数N 时，发射头振动板运动满足：

x = A （ n） sinωt （1）

式中t ∈［ （ n - 1） T ， nT ］ ， A （ n）是第n 个周期内的振幅。

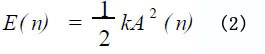
k 是常数， E（ n） 是第n 个周期内振动板的机械能。

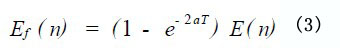
a 是一个与衰减有关的常系数， Ef （ n） 第n 个周期内振动板损耗的机械能。

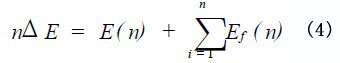
ΔE 是压电晶片每次施加的能量。

在n > N 时， 发射头振动板运动能量满足：

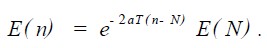
1. 3 接收信号超声波包络

发射头产生的超声波遇到不同介质就会产生回波，接收头把回波转变成电能，产生接收信号。 现分析超声波垂直入射到墙壁面时的接收信号，接收信号超声波包络由起振阶段和衰减阶段两部分组成，如图1。

接收信号与回波超声包络的各正弦波幅值关系是：

式中W R 是接收信号包络峰值，W Echo 是回波包络峰值， H 是回波的单位冲击响应。

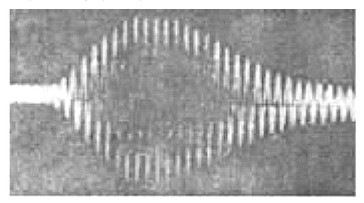
图1 实际接收信号（ N = 5）

从图1 中可看出， 接受信号包络从起振到峰值的时间要小于从峰值衰减至噪声幅值的时间。 实际总长度接近1. 5 ~ 2 ms ，而从起振到包络峰值只需250μs 左右，即9 ~ 12 个T ， T = 25μs.

根据发射的超声波能量特点， 得出接收信号每个周期能量的表达式， 设每个周期内的正弦波是标准正弦波且发射头振动板尚未达稳定振动状态。

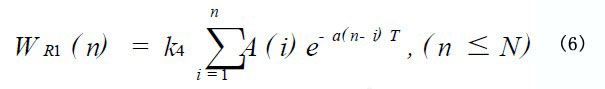
N 是发射头激励脉冲数。

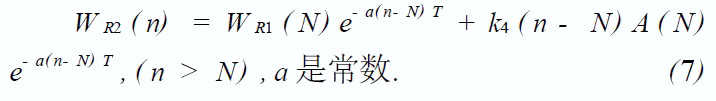
由（6） 、（7） 式知：在N ， a 一定的情况下，每个反射面产生的回波作用接收头得到的接收信号经归一化后是相同的。 为了便于取阈值，分析接收信号包络的特性与n、N 的关系是必要的。 首先找出定值a ，方法是取N = 5 ， a值在一定范围内变化得到多幅仿真图，经比较a = 5 000/ s 时得到的图2 与图1 接近。 根据得到的a值可仿真N = 12 时的接收信号，见图3.

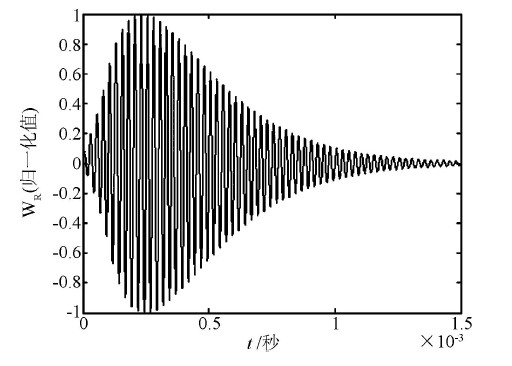
图2 接收信号仿真（ N = 5 ， a = 5 000/ s）

图3 接收信号仿真（ N = 12 ， a = 5 000/ s）

2 阈值和分辨率

阈值的选取，决定本测距系统的测量精度。 由于回波的能量大小受入射角、反射面大小、形状和材质、空气的湿度和温度等因素决定，为了较精确地测量文献中机器人与墙壁之间的距离，下面只针对超声波垂直入射墙壁，接受信号的大小进行分析。

在测量时，一旦有干扰物挡住超声波到墙壁的行进路径，则墙壁返回的信号将减弱，过高的阈值可能测不到墙壁回波信号，动态阈值因无规律可循而无法使用，故此阈值采用小固定值，因接收信号中的噪声峰值较稳定，固定阈值取3~5 倍噪声峰值。 由于墙壁回波信号不确定地高低变化，在标定测量参数时，用示波器采集信号，以接收信号包络峰值的0. 5 倍处（即图2 中n = 4 或5 处的时间） 作为距离信息。 这样处理的目的是：