矢量分析仪原理详解

数据窗是解决泄漏问题的一个常用方法。FFT 并不是误差的起因，它能够对时间记录中的信号生成"精确"的频谱。导致误差的罪魁祸首是时间记录之间的非周期性信号特性。数据窗使用窗功能修改时域数据使其变成按时间记录为周期。实际上，它强迫波形在时间记录的两端变成零。这由给时间记录乘以加权的窗函数来实现。窗对时域中的数据进行变形，以改善其在频域中的精度。参见图 8。

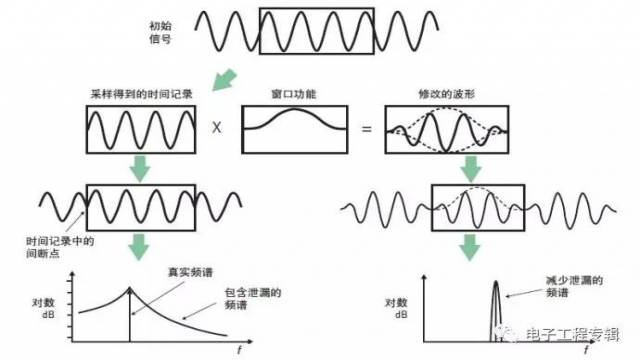
图 8. 窗功能通过修改时域波形，减少频域中的泄漏误差。

Agilent 89600B VSA 基于用户选定的测量类型假设用户的优先考虑情况，自动选择适合的窗滤波器。不过，如果希望手动改变窗类型，你可以从几种内置的窗类型中选择。每个窗功能及其相关的 RBW 滤波器形状拥有各自的优势和劣势。某窗类型可能改善了幅度精度并减少了"泄漏"，但代价却是减小了频率分辨率。因为每种窗类型产生不同的测量结果 ( 差异大小取决于输入信号的特性以及触发方式 )，所以你需要针对所进行的测量谨慎选择适合的窗类型。表 1 总结了四种常见的窗类型及其用途。

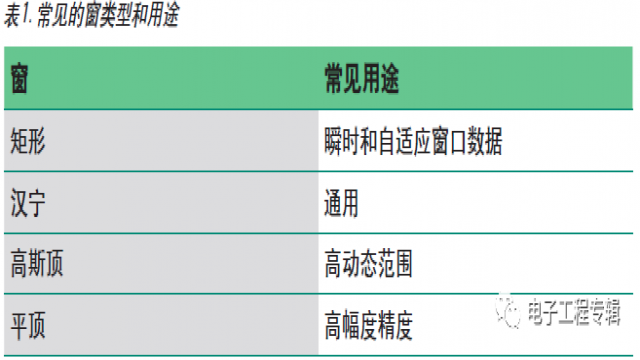
窗滤波器对分辨率带宽的影响

在传统的扫频调谐分析中，最后的 IF 滤波器决定了分辨率带宽。在 FFT分析中，窗类型决定了分辨率带宽滤波形状。窗类型和时间记录长度决定了分辨率带宽滤波的宽度。因此，对于给定的窗口类型，分辨率带宽的改变将直接影响时间记录长度。反之，时间记录长度的改变也会导致分辨率带宽变化，如下式所示 :

RBW = 归一化的 ENBW/T

其中 ENBW = 等效噪声带宽

RBW = 分辨率带宽

T = 时间记录长度

等效噪声带宽 (ENBW) 是窗口滤波器与理想矩形滤波器进行比较的因数。它等效于通过与窗口滤波器相同数量 ( 功率 ) 白噪声时矩形滤波器的带宽。表1-2 列出了几种窗类型的归一化 ENBW 值。ENBW 等于归一化的 ENBW 除以时间记录长度。例如，0.5 秒时间记录长度的汉宁窗的 ENBW 为 3 Hz (1.5 Hz-s/0.5 s)。

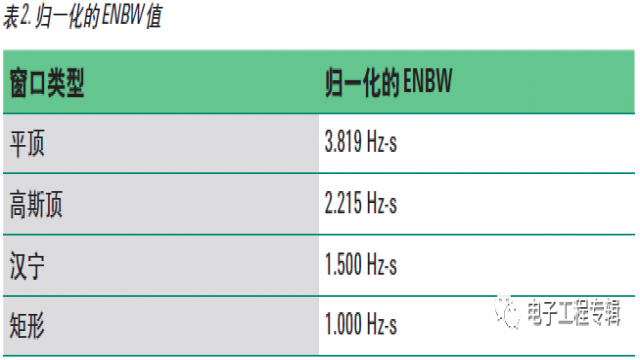
快速傅立叶变换（FFT）分析

信号现在已经准备好进行 FFT 变换。FFT 是针对记录以特殊方式处理采样数据的算法。FFT 不像 ADC 转换那样对每个数据采样进行处理，而是等到获得一定数量的样本 (N) ( 称为时间记录 ) 之后，再将整个数据块进行转换。参见图 9。换句话说，在 FFT 中，输入是 N 个样本的时间记录，输出是 N 个样本的频谱。

FFT 的速度取决于对称性或未落入限定的 2 的 N 次方的重复采样值。FFT 分析的典型记录长度为 1024 (210) 个采样点。FFT 生成的频谱在采样频率?s/2 ( 这个值称为"折叠频率"，??) 两侧对称。因此，输出记录的前半段包含的是冗余信息，所以只有后半段被保留，即采样点 0 至 N/2。这表明输出记录的有效长度为 (N/2) + 1。必须给 N/2 加 1，因为 FFT 包含零点线，输出从 0 Hz 至 N/2 Hz 的结果。这些都是包括幅度和相位信息的复数数据点。

理论上，FFT 算法输出的是从 0 Hz 到 ?（?） 范围内的 (N/2) +1 个频率点。不过实际中，因为需要使用预防混叠的保护带，所以通常不是所有点都被显示出来。如上所述，保护带 ( 大约在 ?s 的 40% 至 50% 之间 ) 不显示，因为它可能被混叠分量破坏。例如，对于记录长度为 2048 的样本，会产生 1025 个唯一的复数频率点，而实际上只有 801 个频率点会被显示出来。

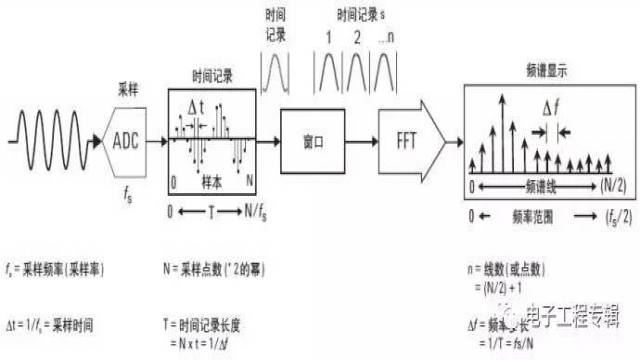
图 9. FFT 的基本关系

这些频域点被称为"线 (line)"或"点 (bin)"，通常编号从 0 到 N/2 。这些点相当于一组滤波器分析中的单独的滤波器 / 检波器输出。点 0 包含输入信号中的 DC 电平，称为 DC 点。这些点在频率上的间割是相通的，频率步长 (Δf) 是测量时间记录长度 (T) 的倒数，即 Δf = 1/T。时间记录长度 (T) 由采样率 (fs) 和时间记录中的采样点数 (N) 来确定 : T = N/fs。每个点的频率 (fn) 如下 :

fn = nfs/N

其中，n 为点数

最后一个点包含最高频率 fs/2。因此 FFT 的频率范围从 0 Hz 到 fs/2。注意 FFT 最高的频率范围不是 FFT 算法的频率上限 fmax，并且可能不同于最高的点频率。

实时带宽

因为 FFT 分析在获得至少一个时间记录之前不能计算出有效的频域结果，所以时间记录长度决定了初始测量花费的时间。例如，使用 1 kHz 扫宽的 400线测量需要 400 ms 的时间记录 ; 3200 线测量需要 3.2 s 的时间记录。捕获的数据时间长度与 FFT 计算引擎的处理速度无关。

在时间记录被捕获之后，处理速度成为一个问题。计算 FFT、调整格式和显示数据结果所用的时间长短决定了处理的速度和显示更新的速率。处理速度的重要性体现在两个方面。首先