矢量分析仪原理详解

?s 上，保护最宽频率扫宽上的分析。在模拟滤波器之后的数字滤波器，为较窄的、用户定义的扫宽提供抗混叠能力。

当抗混叠涉及带限信号，并使用示波器作为 VSA 软件前端时，还必须采取额外的预防措施。

下一个限制小分辨率带宽分析的复杂因素来源于 FFT 算法自身的本质特性,FFT 实质上是一个基带转换。这意味着 FFT 频率范围从 0 Hz ( 或 DC) 开始，一直到某个最大频率 (fs/2) 结束。在小频段需要被分析的测量情况中，这可能是一个重大限制。例如，如果测量前端的采样率为 10 MHz，频率范围将从 0 Hz 到 5 MHz (fs/2)。如果时间样本数量 (N) 为 1024，那么频率分辨率将为 9.8 kHz (fs/N)。这意味着接近 9.8 kHz 的频率可能无法分辨。

如前所述，可以通过改变采样率来控制频率扫宽，但是由于扫描范围的起始频率是 DC，所以分辨率仍然受到限制。频率分辨率可以任意提高，但是付出的代价是最高频率的降低。这些限制的解决方法是带宽选择分析，又称为"缩放操作"或"缩放模式"。缩放操作使您可以在保持中心频率不变的情况下减小频率扫宽。这点非常有用，因为你可以分析和查看远离 0 Hz 的小频率分量。缩放操作允许你将测量焦点放在测量前端频率范围内的任意频率点处 ( 图 7)。

缩放操作是一个数字正交混频、数字滤波和抽取重采样的过程。感兴趣的频率扫宽与缩放扫宽中心频率 (?z) 上的复数正弦波与相混频，从而使频率扫宽下变频到基带 ; 然后针对该特定扫宽对信号进行滤波和抽取 重采样，移除所有带外频率。这就是在 IF ( 或基带 ) 上的频带转换信号，有时称为"缩放时间"或"IF 时间"。也就是说，它是信号的时域表示应为它出现在接收机的中频带。在本章结尾的"时域显示"部分我们将对缩放测量做进一步讨论。

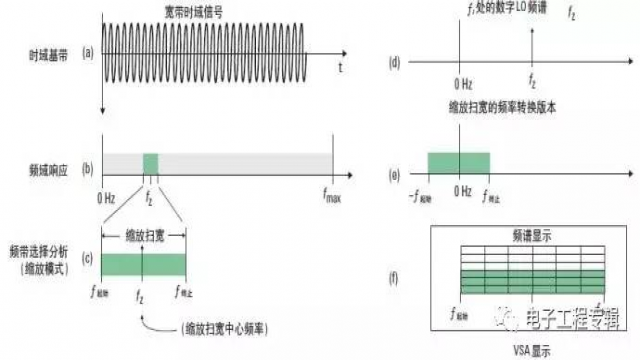
图 7. 频带选择分析 ( 或缩放模式 ): (a) 被测宽带信号，(b) 被测信号的频谱，(c) 选择的缩放扫宽和中心频率，(d) 数字 LO 频谱 ( 位于缩放中心频率处 )，(e) 频率扫宽下变频到基带，(f) 显示频谱注释经过调整，以显示正确的扫宽和中心频率

样本存储器

数字抽取滤波器的输出代表的是带宽受限的数字化的模拟时域输入信号。这个数字数据流被捕获到样本存储器中 ( 图 4)。样本存储器是一个循环的 FIFO ( 先进先出 ) 的缓存器，它收集单个的数据采样，形成被称作时间记录的数据块，再由 DSP 进行进一步数据处理。填充时间记录所需的时间长度与并联滤波器分析中的初始建立时间类似。样本存储器所收集的时间数据是用来产生各个测量结果 ( 无论是频域、时域或调制域 ) 的基础数据。

时域数据校正

为了提供更精确的数据结果，VSA 软件通过均衡滤波器进行时间数据校正。在矢量分析中，时间数据的精度非常重要。它不仅是所有解调测量的基础，还直接用于诸如瞬时功率随时间变化的测量中。时间数据校正是创建接近理想的频带限制信号过程中的最后一步。虽然数字滤波器和重采样算法提供了任意带宽 ( 采样率和扫宽 ) 的支持，但是时域校正决定信号路径的最后通带特性。如果模拟和数字信号路径是理想的，那么就没有必要进行时域校正。时域校正起均衡滤波器的作用，以补偿通带内的缺损。这些缺损来源于多处。射频部分中的 IF 滤波器、模拟抗混叠滤波器、抽取滤波器和重采样滤波器都会对所选扫宽内的通频段纹波和相位非线性特性有所贡献。

在设计均衡滤波器时，首先要基于测量前端的配置，从自校准数据中提取关于模拟信号路径的信息。使用这些数据产生频域校正输出显示结果。一旦计算出模拟校正矢量，结果将被修改以便把抽取和重采样滤波器的影响包括在内。

最后频率响应的计算在选定了扫宽后进行，因为它决定了抽取滤波阶段的数量和重采样率。复合的校正矢量充当适用于时间数据的数字均衡滤波器的设计基础。

数据窗口，泄漏和分辨率带宽

FFT 假设将要处理的信号从一个时间记录到另一个是周期性的。但大部分信号不是按时间记录周期重复的，两个时间记录之间会出现不连续。因此，这个 FFT 假设条件对大多数测量是无效的，必须假设存在不连续性。如果信号不是按时间记录周期重复，那么 FFT 将不能准确估算频率分量。最终的效果是产生所谓的"泄漏"现象，就是能量从单一频率扩散到一段广泛的频率上。模拟扫频调谐信号分析在扫描速度对于滤波器带宽来说太快时将产生类似的幅度和扩散误差。

数据窗是解决泄漏问题的一个常用方法。FFT 并不是误差的起因，它能够对时间记录中的信号生成"精确"的频谱。导致误差的罪魁祸首是时间记录之间的非周期性信号特性