一种并行BCH编解码的设计与实现(下)

接上篇
2.2 计算错误位置多项式[4]
在上一步的伴随式的计算中，若 Si 的值不全为0，则 表示信息在传输过程中发生了错误，需要求出错误位置多项
式，有关关键方程[4-5]这里不再赘述，设位置多项式为：

则回到步骤2。
2.3 求解错误位置（并行钱氏搜索）
在 [ 5 ] 中 所 涉 及 到 的 是 钱 氏 搜 索 的 基 本 算 法 ， 最 大 的 缺 陷 就 是 一 次 只 能 寻 找 一 个 位 置 ， 本 文 使 用 的 码 字 是
（4304,4096,16），码长为4304，完成一次钱氏搜索需要消 耗4096个时钟周期，是难以容忍的，所以本文在原来的算 法上进行了改进，在同样的时间内能够完成对8个位置的搜 索，完成一次钱氏搜索的时间降低为原来的八分之一，即538个周期。
由编解码理论知

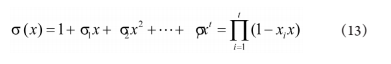
本文中的BCH（4304,4096,16）是一个缩短码，原码是（8191,7983,16）。所以在使用钱氏搜索寻找错误位置的时候，并不需要把全部的元素都搜索一遍，本文所用的码字相 对于原码缩短了3387位，只需要从第3387位开始搜索即可， 从而在很大程度上提高了钱氏搜索的效率。

本文设计的并行钱氏搜索电路结构如图6所示。
对图6的描述如下： 第一个时钟周期， 二路选择器把 最左边有限域乘法器得出的结果存入寄存器中，之后每一 个周期，二路选择器选择后面反馈过来的数据。现在只看 第一排，有8个有限域乘法器，且每一个乘法器计算出来之 后都会送到下面的加法器中进行运算，所以实现了8位并行 计算的功能。一共有15排这样的有限域乘法器，计算过程 跟第一排完全相似。加法器得出的结果用 表示，如果输出 结果为0表示对应的位没有出错，如果为1证明对应的位是 错误的，也就找到了错误的位置。假如搜索到8位都没有出 错，那么输出结果为00000000，如果全部出错，输出结果为11111111。

3 BCH编译码器的仿真与分析
数学软件Matlab嵌有BCH编译码函数，可以完成计算 BCH码的生成多项式、对数据进行编码译码等功能。ISE中 的仿真结果出来后，与matlab中生成的数据进行对比，可以 验证仿真结果的正确与否。
3.1 BCH编码器测试结果与分析
首先向matlab程序输入4096Byte的数据，对这4096Byte 的数据进行编码，将编码后的校验位与通过所设计的BCH 编码器编码后产生的校验位进行对比，以此验证编码器的功 能。若两者生成的校验位相同，则认为所设计的BCH编码器 能够正确实现其功能。假 设 输 入 的 4 0 9 6 By t e 的 数 据 全 部 为 8' b11111111 ， 由mat l ab 程序计算得到的校验位如下： 0 1 1 0 0 1 0 1 0 0 1 0 1 0 0 0

00010000 01101110 01110111 01111111 00000100 00001000
11111001 11000101 10100011 01100000 10110110 11011011
00101111 10001010 11111101 00011100 10100110 00011111
00011011 01000011 11100001 11011111 10001111 11010001
利 用 I S E 对 B C H 编 码 器 进 行 仿 真 ， 得 到 的 结 果 如 图 7（177页）所示。
对比公式4中得到的结果和matlab程序得到的结果，发现两者结果相同，因此，可以证明所设计的BCH编码器是正确的。
3.2 BCH译码器的测试结果与分析
当我们把信息位和校验位放在一块进行译码的时候，得到的结果如图所示，错误位置值的八位数据全部为0,如图8（177页）所示。
这 时 我 们 故 意 把 校 验 位 的 最 后 8 位 1 1 0 1 0 0 0 1 改 为11011110，然后进行与上面同样的操作，得到的结果如图9
所示。如图9（177页）所示发生错误的8位对应的错误位置的 数据位为00001111，其他错误位置的数据位均为00000000， 由此证明错误位置已经找到，只要把发生错误的数据位与错 误位置的数据位进行异或就能得到正确的数据。以 上 测 试 可 以 得 出 ， 我 们 设 计 的 B C H 译 码 器 是 正 确 的，能够找到错误的位置并进行修正。

4  结束语
本文首先测试了并行编码，将得出的数据与matlab中产 生的编码数据进行对比，发现两者的结果完全一致，然后对 解码进行同样的过程，发现所测试的数据也是正确的。但有 一个问题尚未解决，那就是测试的数据量比较小，并不能够 完全保证所写的程序是正确的，而且当错误的个数超出纠错 能力的时候，能够发现错误，但是无法纠正过来。

参考文献:
[1]王新梅，肖国镇，纠错码—原理与方法[M]. 西安：西安电子科技大学 出版社，2001.
[2]王杰．NAND  Flash主控中BCH编译码器的研究和ASIC实现［D］
．浙江：浙江大学电气学院，2010．
[3]胡珊珊. B-T2系统中BCH译码器的设计与实现[D]. 武汉：武汉理工大 学信息工程学院，
2012. [4]唐建军，纪越峰，超高速BCH码解码改进算法研究[J].北京邮电大学 学报，2004,25
(9):21-27.
[ 5 ] Y n n i  C h e n , K e s h a b  k . P a r h i . A r e a  E f f i c i e n t  P a r a l l e l D e c o d e r  A r c h i t e c t u r e  f o r  L o n g  B C H  C o d e
s [ J ] . I E E E International Conference on Acoustics,Speech,and Signal
Processing,2004,5(4):481-483.
[6]殷民.  闪存控制器中差错控制编码研究[D]. 合肥：中国科学技术大学 信息科学技术学院，
2012.
[7]  Yin, Min;Xie,  Menwang;Yi,Bo. Optimized  algorithms  for binary BCH codes
[C].Beijing: Circuits  and Systems (ISCAS), 2013 IEEE International  Symposium on
,2013.
[8]Wu,Tao, Efficient Recording of Parallel  Chien Search Results of BCH Code by
Three-Staged and  Group-Sorted  Circuit[C]. chengdu:Computational Science and Engineering(CSE),2014. [9]Zhu,Yuelin,An  Intellectual  Biography[D].Boston:Harvard
University,2002.