双目摄像技术分析--突破光学与尺寸的极限

迭代最近点

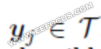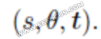此刻，假设我们没有外点。我们期望对于任意，存在最近点。如果我们使用一个合理的转换估计，距离不能太大。注意点的索引依赖于j, 但也依赖于特定的转换参数，记最近点索引为，假设我们估计的转换欢喜为。然后我们迭代地精细化估计结果：(a)转换S中的点；(b)逐一找到T中对应的最近点；以及(C)最小二乘法重新估计转换参数。这催生了一个迭代算法，根据文献 Besl and McKay (1992),称为迭代最近点算法iterated closestpoints。该算法可以明确地收敛到正确答案（钓寒江雪翻译）。

实际应用中，它确实可以。两个点集可以助其改善其性能。首先，重估计过程不需要收敛以使算法有用。例如，我们不需要完整地估计转换关系，我们做一次梯度下降。这稍微改善了转换关系，且修改了最近点映射关系。其次，我们不需要再最小化过程中使用全部的点。特殊地，如果最近点相对较远，最好在下一步的最小2乘法中抛弃这些点。这会使算法更鲁棒。

你可能会认为与其说这是个算法不如说是个算法模板；大量特征可以被成功地修改。例如，它可以用来在数据结构中小心地加速保持对最近点的跟踪。另一个例子，一个可选的用于改善鲁棒性的策略，是使用M估计器取代最小二乘误差项。事实上，该算法不需要S和T的点集。例如，它相对直接地用于S是网格点，T是点集的案例（Besl and McKay 1992）。另外，有良好的证据表明我们优化的关于(s, θ, t)的目标函数在实际应用中性能良好。例如，虽然它不是可微的（因为最近点改变，导致微分步长变化），2阶方法如牛顿方法或者LBFGS在实际引用中事实上表现更好。

通过映射关系搜索转换关系

迭代最近点重复估计源集于目标集的映射关系，然后用以估计转换关系。就我们所见，该搜索方法面临很多局部极小值。另一个方法是搜索映射空间。这看起来似乎没有前途，因为有大量的映射关系，但是在刚性物体的案例中，较小的映射集足以配准整个物体。另一个直接考虑映射的优势是我们可以直接使用标记进行作用而不是点。例如，我们映射中放置线段，角，甚至如斑点（blobs）点状特征。这类标记可能改变细节，但对整个算法影响微小。

很小的源标记集与目标标记集进行映射，足以估计转换关系。集合的尺寸依赖于转换关系及标记本身。我们参考可用于计算转换关系的称谓帧支持群frame-bearing group一群标记。表12.1给出了2D-2D帧支持群的例子，且表12.02给出了3D到3D案例的例子。这也将在未来的运用中进一步拓展。

现在我们假设我们在源和目标中有帧支持群。进一步，如果我们有标记集的映射关系，我们可以计算源之于目标的相应的转换关系（钓寒江雪翻译）。只能有一个可能的映射关系。例如，如果群是先或者点，我们只能把源线（点）放置在与目标线（点）映射的位置。但是可能有多种可能的映射；例如群由3个点组成，但是有6种可能性。

如果一个群或者映射错误，大部分的源标记将转换到远离目标的位置。但是如果正确，很多或者大部转换过的源标记将落在目标标记附近。这意味着我们可以用RANSAC（10.4.2），重复地使用如下步骤，分析结果：

• 为目标和源随机选择帧支持群，
• 计算源与目标单元的映射关系（如果有多个，我们随机选择），然后计算转换关系。
• 使用该转换关系转换源集没，并与目标进行比较打分只。

如果我们实施足够多次，我们极大可能可以在好的群之间获得好的映射结果，且我们也可以检查每个分数用以分辨优劣。从好的映射关系，我们可以分辨源与目标的匹配对，最终根据最小2乘法计算转换关系。

应用：建立图像拼接

一个拍摄大而壮观的目标的细节的方法是拍摄很多张小的图像，并将其拼接到一起。过去的做法常常是将照片冲印，然后堆叠贴在软木板上，用以吻合。这引入了图像拼接，一系列重叠的图像。图像拼接现在能用数字图像配准的方法实施。

表1 3D-3D帧支持群.假设我们在源和目标中都有一个群，且有一个映射关系；从而，我们可以唯一地估计转换关系。

Figure 10 左图，机场上空航拍视频帧。这些帧被矫正并拼接在右图，其中显示（a）全局可见结构（b）飞机飞行路径。这个图最作为Figure1发表在“Video Indexing Based on Mosaic Representations,”by M. Irani and P. Anandan, Proc. IEEE, v86 n5, 1998, _c IEEE, 1998.

一个应用是创建大型图像。也有几个其他重要的应用。例如，假设我们用在飞机垂直安装的一个的摄像机拍摄了一些图像（钓寒江雪翻译）；然后如果我们一帧一帧配准这些图像，我们不但可以得到飞机可见的图像，还可以呈现飞机的路径，如图Figure 12.1所示。