基于AD5933的高精度生物阻抗测量方法*

摘要： 本文利用阻抗测量芯片AD5933，以单片机作为控制器，依据此芯片比例法测量原理、DFT解调原理结合软件校准和软件补偿的算法，实现了一种高精度生物阻抗测量方法。实验结果表明，此方法有效提高精度，测量阻抗幅值的相对误差小于0.5%，相位绝对误差小于0.7°。

关键词： 生物阻抗；比例测量；DFT数字解调；AD5933

*国家自然科学基金项目(No.60174032，60674111)
　　2008年4月29日收到本文修改稿。林凌，副教授，研究方向为生物医学信号检测与处理、生物医学工程。

引言

　　生物电阻抗技术是利用生物组织与器官的电特性及其变化规律提取与人体生理、病理状况相关的生物医学信息的检测技术。其基本测量方式是通过体表电极向检测对象施加安全的激励电流，并使用体表电极检测相应的电压变化，获取相关信息。该方法具有无创、无害、廉价的优点。目前针对生物阻抗测量系统的研究和文章很多，主要集中在对整个测量系统某组成部分的设计。显然，这些研究和设计工作均在某一方面对生物阻抗测量系统的精度提高做出了贡献，但是单一的方法对精度的提高有限，本文采用ADI公司的高度集成的阻抗测量芯片AD5933设计了一种精度高的阻抗测量方法，利用比例测量，DFT数字解调，软件校准和补偿四项技术，整体上提高了系统的测量精度。

比例测量方法

　　对电阻的测量，通常使用伏安法，生物阻抗测量也是基于伏安法的原理。即已知一个元件的电阻等于此元件两端的电压降与流过其电流的比值，RX=UX/IX。然而在实际测量中往往使用比例测量的方法，在被测回路中串入采样电阻RS，有IX=US/RS，因此：RX =UX/IX=RS×UX/US，这样就把电阻的测量转换成为两电压之比的测量，降低了对电压源US的准确度和稳定度的要求，测量结果的精确度只与参比电阻的精度有关。比例测量的具体电路非常简单，如图1所示，用一只运算放大器接成电压并联负反馈结构即可。

图1　比例法测量电阻的原理图

　　本文采用的阻抗测量芯片AD5933利用了上述比例测量的原理，测量电路如图2所示。利用DDS产生的正弦交流信号作为激励源以获得阻抗的完整信息，待测阻抗可等效为电容和电导的并联模式，即YX=GX+jCX=AX<φ。在理想状态下不考虑放大器等电路引起的幅值和相位的变化，设激励信号U1=U1msinwt，I=U1×YX，则响应信号U2=-I×RS=-U1×YX×RS=-U1m×RS×AXsin(wt+j)，其中j被测电导的相位，AX为被测电导幅值，RS为参比电阻。只要将U2与U1做比较就可以得到待测阻抗的信息，避免了电压源不稳定带来的误差，测量结果的精度取决于参比电阻的精度。

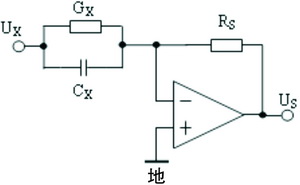
图2　AD5933比例法测量生物阻抗原理图

DFT数字解调

　　上述响应信号U2包含了阻抗的信息，与U1进行比较可以获得阻抗的信息，但是由于U2(调制信号)是U1(载波)经过阻抗的调制得到的，U2中含有载频信息，不利于后面的阻抗信息提取，所以需将对响应信号U2解调，即去除载频w，还原为零基带信号。目前阻抗测量系统中常用的解调方式有硬件解调：整流滤波、开关解调、模拟乘法器、数字解调。模拟乘法器解调是常用的方法之一，它利用正交解调原理，具有电路简单，测量速度快且适合于较高较宽的频率范围内工作的优点。
利用乘法器正交解调的过程描述如下：假设要将上述响应信号解调，首先利用乘法器将响应信号(U2=-U1m×RS×AXsin(wt+j))与一对正交本振(U1=U1msinwt，U3= U1mcoswt)相乘(本振信号要求与载波同频同相，并且两个本振信号严格正交)，然后利用积化和差公式将载频与基频分离，再通过滤波或积分运算去掉载频，将信号变为基频。

　　正交本振信号与上述响应信号相乘，利用三角函数里的积化和差公式，得到两路信号Uo1和Uo2，将载频信号与基带信号分离。

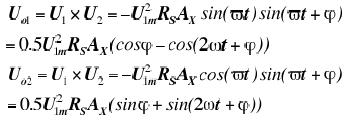
　　将上述两路信号在周期T时间上做积分并求平均值去除载频。

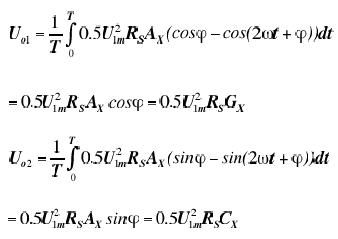
　　以上过程完成了正交解调，显然Uo1，Uo2中已经去除了载波，并且仍然包含被测电阻的实部和虚部信息，只要与电压源幅值信息比较就可以得到被测阻抗的完整信息。
类似的，AD5933也是基于正交解调的原理，对ADC采样数据做离散傅立叶变换(数字正交解调)，也即1024个数组成的数字序列与正交向量相乘再求和的过程，如下式所示：
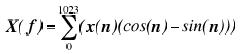        (1)
　　利用DFT数字正交解调与利用乘法器正交解调相比的优势在于：正交解调方法要求本振和信号载波同频同相，否则解调后的信号会产生频差和相差，不利于信号恢复。利用模拟乘法器方法解调，很难实现载波同步，甚至还要增加模拟锁相环电路，而DFT从算法上严格保证了本振和载波的同频同相。其次正交解调要求两个本振信号完全正交，否则恢复原信号时会产生虚假信号，DFT算法很好的保证两个本振严格正交。DFT算法实现了数字锁相的过程，保证了本振和载波的同频同相，简化了模拟电路，并且求和平均的过程抑制了噪声，调高了信噪比。