A3000过程控制实验系统开发

A3000过程控制实验系统最具工程化特性，可以模拟各种工业现场。本文以工业多容系统中的PID控制为实例，分析单容液位系统、双容液位系统以及三容液位系统对多个容器串联后系统特性的影响，并通过多容液位系统控制实验进行验证。

1 研究的模型范围
工业多容系统各种各样，实际情况比较复杂，有相互竖直连通的，有水平放置通过压力连通的，有大容器也有小容器，有的容器出口还不只一个。然而作为理论研究，应把问题限制在一种特殊的情况下，以便排除各种非关键因素的干扰，从而获得更为清晰的理论。如图1所示。三个容器在竖直方向相叠加，那么上一个出口流量不会受下一个容器液位的影响。实际上，真实的工业系统还有三个容器水平并排放置，那么高液位容器的出口流量就会受低液位容器液位的影响。

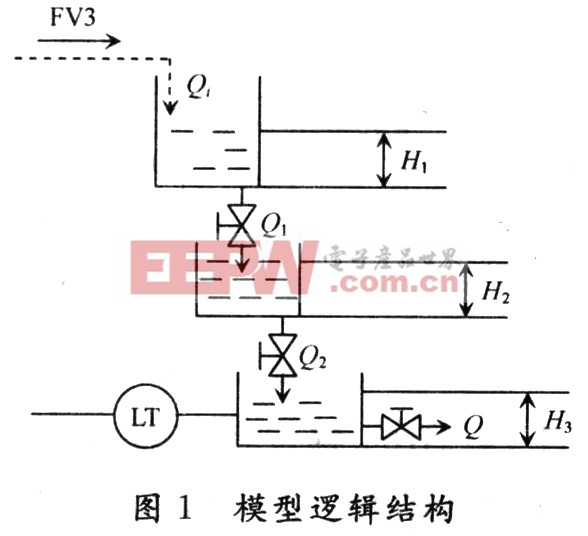
2 数学模型的建立与测定
2．1 系统模型的建立
由于三容系统液位数学模型具有高阶导数，比较复杂，使用直接的公式计算是困难的。这里通过对单容和双容准确模型的计算和分析，然后经验性的推理来解决工业中多容问题，包括三容。
下面按照类递推原理，建立单容、双容、三容系统的数学模型：

随着容器个数的增加，可以根据递推原理，推导出更加复杂的多容系统数学模型，但在这里不再做更多的推导。
2．2 系统模型的测定
不同系统水位阶跃响应曲线如图2～图4所示。
由于三容系统比较复杂，特别是当工业对象特性本身不是简单同样容器竖直叠加时，公式更加复杂，所以这里只给出一个简单的数学模型公式，目的在于通过单容、双容的模型测量，获得一个向多容积系统控制推导的经验方法。

3 多容系统的PID控制推导
单容实验时，利用数字模型调整PID值，分别在P=10，I=100 s，D=0 s时获得了比较好的结果。
双容实验时，利用数学模型调整PID值，分别在P=5，I=200 s，D=0 s时获得了比较好的结果。
对于这种二阶函数，系统稳定时间与其惯性时间有一定关系，而这个时间和PID的积分时间成一个等指数关系。随着容器的串联，导致时间成指数增加，肯定会比线性加倍的方式快，推出如下可能的经验公式：

式中：t为容器特性时间；K为与系统有关的比例系数。这样推出：两容串联，其PID积分时间TI=200 s，三容串联，其PID积分时间TI=400 s，四容串联，其TI=800 s。

式中：t为容器特性时间，K为与系统有关的比例系数。
这样推出：两容串联，其PID积分时间TI=270 s，三容串联，其PID积分时间TI=745 s，四容串联，其TI=2 030 s。

4 多容液位系统控制实验验证
4．1 实验验证及控制曲线
P=2．5，I=600 s，D=0 s，PID控制曲线如图5所示。

P=2．5，I=740 s，D=0 s，PID控制曲线如图6所示。

4．2 控制实验结果分析
从结果来看，推出的经验公式如下：
对于具有同样特性的多个容器，如果以竖直方向连通的方式串联，那么可以推导出如下控制方法。如果单容时最好的PID控制参数为P=P0，I=I0，那么对于多容系统，可以有参考的PID控制参数：

式中：n=1为单容系统，特例。对于n=2，n=3，本文进行了探讨。由于条件有限，没有对n超过3的情况进行验证，希望在以后的工作中能对其进行进一步的验证，使之能被应用于更多容器串联的系统。另外的情况是如果各个容器特性不一样，并且差异不是很大，则可以通过参数修正的方法进行修改。当然，也需要进行大量的验证。这里的结论只是希望能为加快参数选优的过程提供一个参考。

5 结 语
多容液位系统PID控制的研究首先对其建立数学模型，并对多容系统的PID控制进行推导，得出PID对应的最佳数值，最后在通过多容液位系统控制实验进行验证，分析结果可作为对加快参数选优过程的一个参考。