一种处理金属和介质混合结构连接边界的新方法

0 引言
由金属和均匀介质组成的混合结构在雷达散射、天线、微波工程等众多领域都有着广泛的应用。采用矩量法求解由此类问题得到的表面积分方程，是一种广泛而行之有效的数值分析方法。应用等效原理，介质散射问题可以等效为均匀媒质中的外问题和内问题进行分析。最早由Harrington等人给出介质散射体的混合场积分方程，而Umashankar等则给出了任意形状介质散射体的RWG矩量法求解过程。Medgyesi-Mitschang等人提出的广义矩量法能够适用多种介质构成的混合结构。该方法在不同介质区域内的边界表面两侧分别引入电流层和磁流层，得到广义的阻抗矩阵，通过联系边界表面两侧未知电流、磁流的关系来消去非独立的方程组。这样的处理方法具有一般性，且数值实现性好，但是需要占用更多的计算机资源。
对于介质体涂覆有理想金属面的混合结构，一个关键问题就是如何处理介质表面和金属表面的连接边界。在最早Sarkar等人分析此类问题时，将金属面视为可无限接近介质体，但并不接触，这实际是分离的金属和介质结构的一种极限情况。这意味着在与金属面重合的部分介质表面，该模型需要引入一电流层和磁流层，这样会增加待求解的未知数个数，因此仅适用于相对简单、电尺寸小的结构。Su等人在分析二维混合问题时，忽略了跨过金属面和介质面之间的电流。Medgyesi-Mitschang等人给出了处理连接边界的方法，在连接边界处用半个三角基函数展开电流。根据电流连续性，令适当的未知数相等来消去一些方程，得到满秩的矩阵方程。然而，在最初的矩阵填充过程中，必须首先得到非满秩的矩阵方程。另外，对于连接边界半个三角基函数需要给予特殊处理。Yla-Oijala等人给出了基于RWG基函数的介质、金属混合结构的不同类型连接边界的处理方法，仍采用在不同介质区域内的连接边界表面两侧分别引入电流层和磁流层，通过联系边界表面两侧未知电流、磁流的关系来消去非独立的方程组。文献[11]给出了金属介质混合目标的体积分方程矩量法，该方法适合于非均匀介质目标,对于均匀介质目标来讲，未知数与计算量会显著增加。
本文给出一种处理金属和介质混合结构连接边界的新方法。在对模型表面进行三角面元近似后，根据电流连续性和电场、磁场连续性关系，连接边界处的金属面元上的电流与介质面元上的电流呈现相同的特性。这样的一对三角形仍可定义传统的RWG基函数，并在积分方程中归入介质电流统一进行处理，而且最初生成的阻抗矩阵即为满秩的阻抗矩阵。

1 表面积分方程
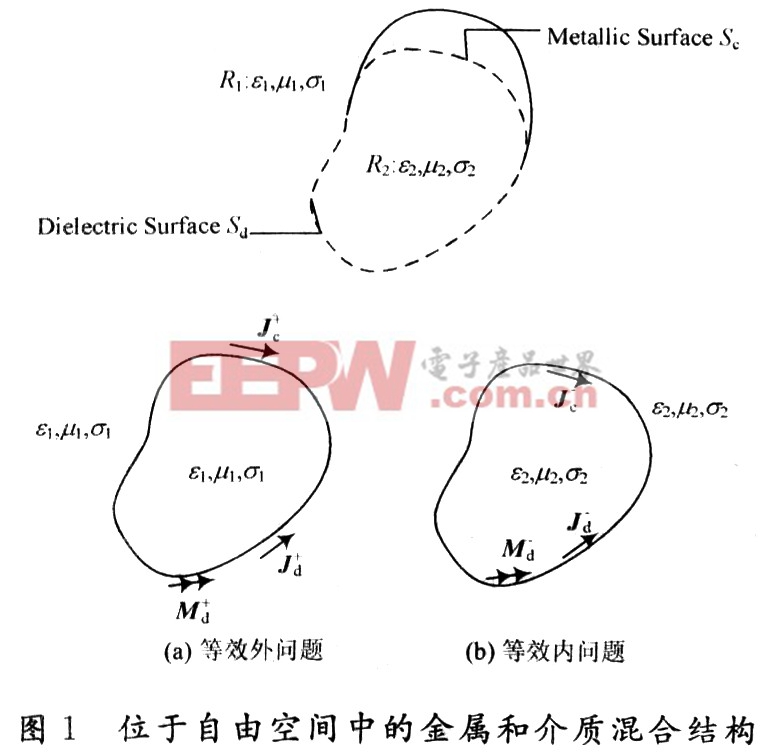
考虑一个位于自由空间中的均匀介质体，介质体的部分外表面覆有理想金属表面，如图1所示。自由空间区域为R1，媒质参数为ε1，μ1，σ1；介质区域为R2，媒质参数为ε2，μ2，σ2。图中实线表示金属面，虚线表示介质面。根据表面等效原理，可以将此问题等效为如图1(a)，图1(b)的外问

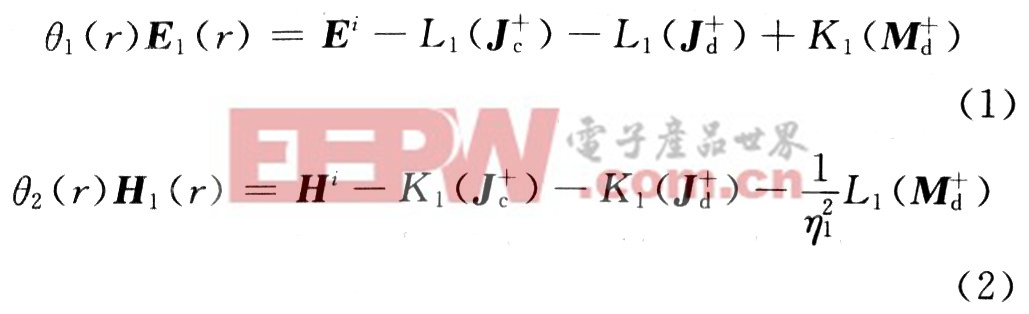
式中：θ1(r)为Heaviside函数来保证边界处的阶越条件。

同理，在区域R2中的电场和磁场可以表示为：

和内表面电流是独立的；在介质面处切向电场和磁场连续，介质面上没有真实的表面电流和磁流存在，因此：

由金属表面切向电场为零和介质表面切向电场、磁场连续的边界条件，可得：

式(11)～(14)被称之为PMCHW(Poggio，Miller，Chang，Harrington，Wu)方程组。将模型表面用三角面元近似，采用RWG基函数将面电流和面磁流展开，根据Galerkin方法可以得到上述方程组的矩阵方程。

2 金属面和介质面的连接边界处理
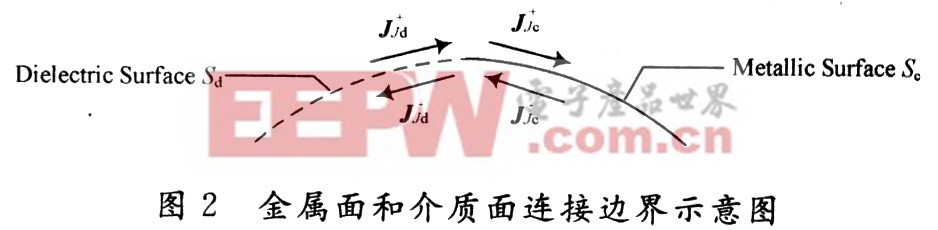
定义金属表面和介质表面连接边界为在对模型进行三角形面元表面近似后，则以连接边界为公共边的一对三角形分别属于金属面和介质面。连接边界处的外表面电流和内表面电流如图2所示。由于金属面上没有磁流存在，因此由连续性条件可知，与金属面相接的介质面处亦不存在磁流。介质面的等效电流和金属面电流有如下关系：

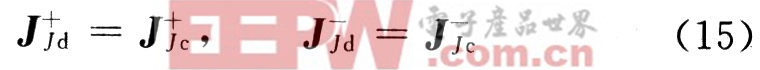
又因为介质面上没有真实的表面电流存在：

，故切向磁场也是连续的。因此，在连接边界处的金属面上，其表面电流、电场和磁场呈现的特性与介质面相同。仍可在以连接边界为公共边的金属三角形面元和介质三角形面元上定义RWG基函数。
这样，可以将所有的三角形公共边划分为三类：
(1)金属公共边。在这些公共边上定义金属面电流密度，包含所有金属面内部的公共边，公共边总数为Nc，由于金属内、外表面电流是独立的，则金属面上电流未知数为2Nc。
(2)介质电公共边。在这些公共边上定义介质面电流密度，包含所有的介质面内部的公共边和连接边界公共边，未知数为Nd+Nj，其中Nd为介质面内部的公共边数目，Nj为连接公共边数目。
(3)介质磁公共边。在这些公共边上定义介质面磁流密度，包含所有的介质面内部公共边，未知数为Nj。在以上定义中，在连接边界上只定义了面电流，面磁流不存在，并将面电流归人介质面电流一类中，这样在积分方程(11)～(14)可作为Jd统一处理。最终得到的满秩阻抗矩阵维数为(2Nc+2Nd+Nj)×(2Nc+2Nd+Nj)，而文献[6]和文献[8]中得到的初始的非满秩矩阵维数分别为[Nc+2(Nc+Nj+Nd)]×[Nc+2(Nc+Nj+Nd)]和(2Nc+2Nd+4Nj)×(2Nc+2Nd+4Nj)。