直方图在抖动分析中的应用

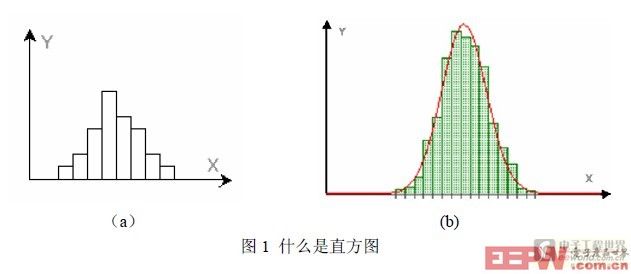
直方图（Histogram）也叫柱状图，它是用一系列宽度相等、高度不等的长方形表示数据的图，如图1(a)所示，长方形的宽度表示数据范围的间隔，长方形的高度表示在给定间隔内的数据数量。在统计学上这是很常用的用来表示样本各组概率分布的一种直观的图表。如果样本容量取得足够大，分组的间隔取得足够小，柱状的直方图就会变成曲线图（图1 b）。这条较为平滑的曲线就是样本总体的密度曲线。它揭示了样本的分布规律。

直方图描绘了数据或者参数值在一个确定范围内出现的概率（如图2），直观的显示了参数的波动状态。在用示波器对波形参数进行测量时，我们可以利用直方图，根据测量结果的统计分析确定产品的一些关键指标，通过大量数据样本的数值范围和分布情况可以验证产品的性能和质量并识别和诊断一些间歇性的问题。尤其是对于随机事件（如噪声或抖动）的了解，它是一个很好的工具。由于在抖动分析中所有信号均包含有随机成分的抖动，因此必须采用统计的手段来分析和检定抖动，而直方图就是最常用的统计分析工具，所以说直方图是抖动分析的基础。

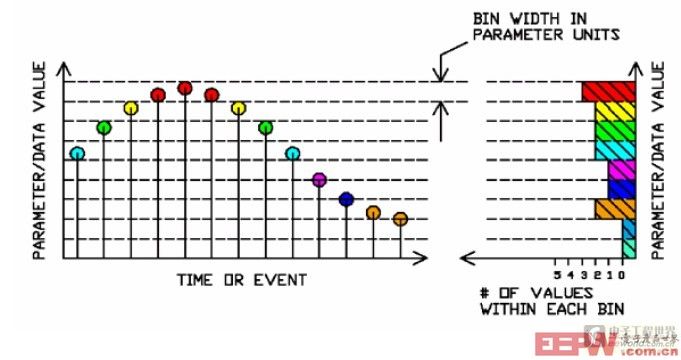
图2 如何得到直方图

描述直方图的主要参数有平均值（mean）、标准偏差（standard deviation）、样本峰-峰值和样本总量。力科示波器包含了所有这些统计参数。

平均值是测得所有值的算术平均，表示测量值的最佳估算结果，即图3中的“mean”。

标准偏差是测量值偏离平均值的平均量，常用σ表示。它决定了直方图的“胖瘦”，标准偏差越大，离散程度越大，图形就越胖。在力科示波器中用“mean ± sdev”表示直方图的标准偏差，如果平均值为0，则标准偏差等于参数的均方根值（rms）。

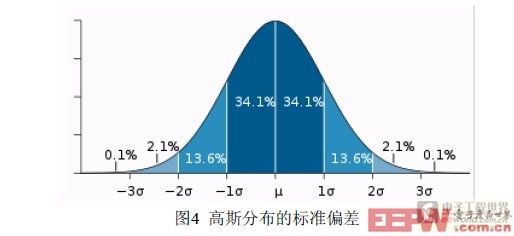
直方图曲线描绘了某个概率分布的概率密度函数（PDF），在数学模型中求这个概率密度函数定积分，即求图1(b)中红色曲线与X轴围成的面积，其结果为1。在实际应用中，很多变量都有近似于高斯分布的概率分布，则其约68%的数值分布在距平均值±1σ之内的范围，约 95% 数值分布在距离平均值有±2σ之内的范围，以及约 99.7% 数值分布在距离平均值有±3σ之内的范围（图4）。

最大值、最小值和峰-峰值：最大值和最小值一般指测量过程中实际观察到的值，峰-峰值（Range）则是最大值与最小值之差。需要指出的是，对确定性信号而言，即使是在相对较短的测量区间内测得的，这些值仍很可能等于其实际的真正值。但对具有高斯分布的随机信号而言，理论上最大值和最小值是没有界限的，因此观察到的峰-峰值一般会随着测量时间（测量样本）的增长而增长。

样本总量是直方图中包括的测量总数，图3中直方图的标签F1指明了这个值，即列表底部的数值。在这一测量实例中，样本总量是频率参数测得的112,345个值。

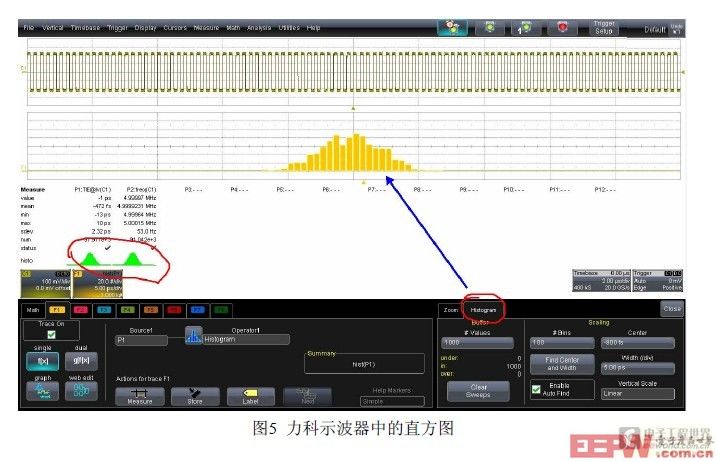
力科WaveRunner以上示波器均标配了直方图功能，既可以快速查看所有参数的小直方图，也可通过运算（math）得到大直方图（图5）。设置样本（buffer）总量和水平分辨率（bin）可以改善直方图的波形并提高测量精度（图6），其中buffer的最大值可以设为20亿！而bin的最大值则可以设为2000！

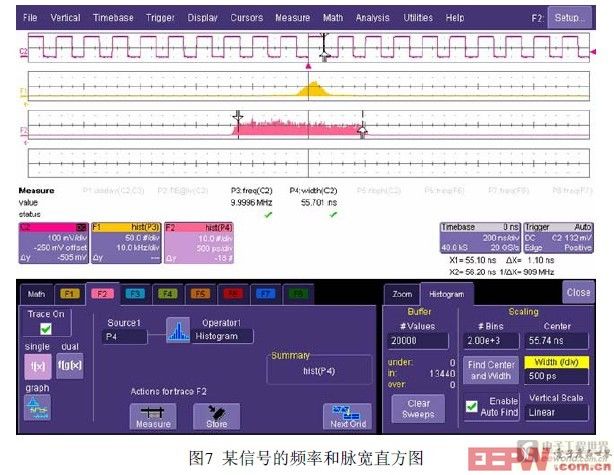
在抖动分析中，参数不同的直方图形状往往揭示了抖动的性质和来源。如图7所示，波形的频率直方图显示为高斯分布（黄色直方图），揭示信号频率仅有受噪声影响的随机抖动，而红色的脉冲宽度直方图为非高斯分布，揭示信号脉宽变化有固有抖动。

以下是几种常见直方图的形状：

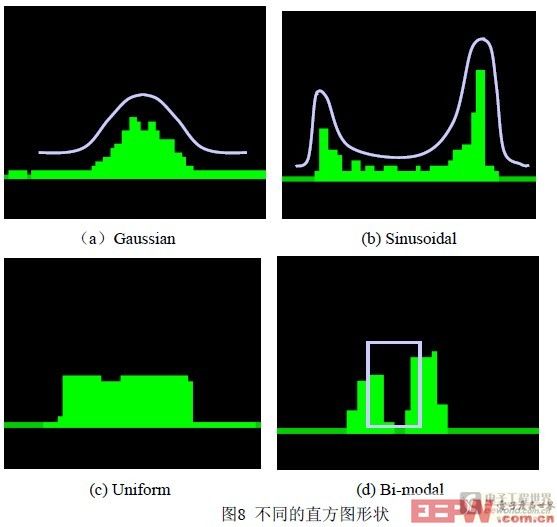
其中，（a）是高斯分布，表明这是一种随机抖动，在大多数电路中其来源主要是系统的热噪声。

(b)是一种正弦曲线抖动或周期抖动，表明抖动中存在周期性的成分，这种抖动一般是由耦合到系统中的外部确定性干扰源引起的，如开关电源噪声或局部RF载波。此外时钟恢复PLL不稳定也可能会导致周期抖动。

(c) 是一种单一分布，可能是由码间干扰（ISI）造成的。而由于连接器、电缆以及通道的信号转换带来的反射、驱动器和接收器的有限带宽造成的抖动是码间干扰的主要成因。其主要特点表现在对码型的依赖性上。每个不同的码型在50%交叉点都有其各自的直方图分布。

(d)是双峰分布，这种抖动极有可能是占空比失真（DCD）贡献的，由于信号上升沿和下降沿的转换速率不同或者波形的判定门限不在50%的交叉点上都有可能造成时钟不对称而带来占空比失真。

可以看出，直方图以非常紧凑的形式传达了大量的信息。在抖动测量和分析中，我们可以使用专用的直方图参数提取信息，这对于我们理解抖动的分布、识别不同的抖动来源，以及系统的调试和失效分析提供了有意义的参考。在随后的文章中，将会有使用直方图测量定时抖动等专题介绍，敬请大家