超声波瓶体厚度检测及其材料分类的研究，保障公共安全

所示。该神经元是一个多输入单输出的非线性元件。

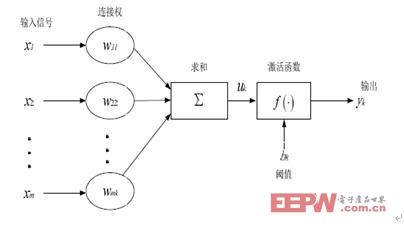
图9 简化的神经元模型

人工神经元模型可以看成是由三个基本要素组成：

• 一组连接权（对应于生物神经元的突触），连接强度由各连接上的权值表示，权值为正表示激励，为负值表示抑制。
• 一个求和单元，用于求取各输入信息的加权和（线性组合）。
• 一个非线性激活函数，起非线性映射作用并限制神经元输出幅度在一定的范围之内。此外还有一个阈值。阈值也被看作是一个输入分量，也就是阈值也是一个权值。在网络的设计中，偏差起着重要的作用，它使得激活函数的图形可以左右移动而增加了解决问题的可能性。

通常所说的人工神经网络结构，主要指它的连接方式。从拓扑结构上考虑，神经网络属于以神经元为节点，以节点间的连接为边的一种图。从连接方式来看，主要有两种，即前馈型神经网络和反馈型网络。一个神经网络的拓扑结构确定后，为了使它具有某种智能特性，必须有相应的学习方法与之配合。权值如何设置是区分不同人工神经网络学习算法的重要特征。一般可以把人工神经网络的学习分为两种类型，即监督学习（有教师学习）和无监督学习（无教师学习）。

本次项目的人工神经网络，设计为两级人工神经网络，其中一级内部神经网络的结构，如图10所示；二级人工神经网络的结构框图，如图11所示：

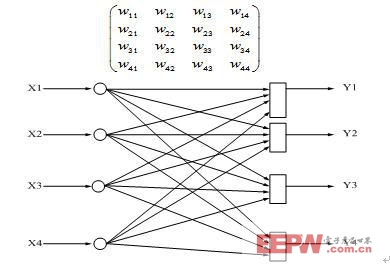
图10 神经网络内部示意图

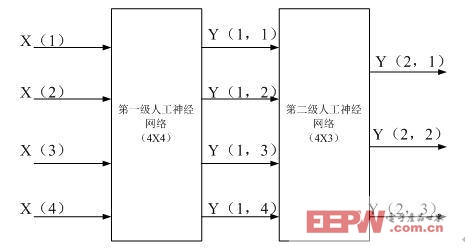
图11 二级人工神经网络的结构框图

我们依据人工神经网络的基本特点，采用乘法器封装的形式进行基本实现，其实现方法，如图12所示：

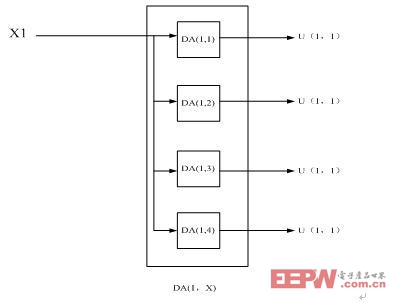
图12 乘法器的封装

那么一级神经网络的FPGA实现，如图13所示：

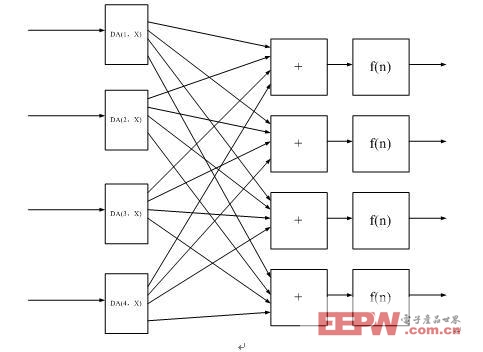
图13 一级人工神经网络的FPGA实现

1. CORDIC计算特殊函数算法简介

如果利用FPGA实现某种数字信号处理算法，并且算法使用了一个非普通的（超越）代数函数，我们可以利用泰勒级数来近似这个函数。

这样问题就简化成一系列的乘法和加法运算了。一种可供考虑的更为有效的方法就是基于坐标旋转数字式计算机（Coordinate Rotation Digital Computer，CORDIC）的算法。CORDIC算法是建立在众多应用基础之上的，如适应性滤波器，FFT，DCT,神经网络。

正式定义的CORDIC算法，如下式所示：

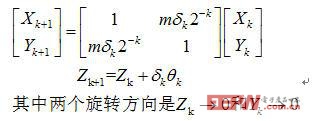
实现CORDIC结构可采用两种基本结构：较为简洁的状态机和高速全流水处理器。

2.3 Restoring（还原）算法简介

Restoring算法是一种线性收敛的除法算法。它的主要思想是首先调整分母并加载分子到余数寄存器中，然后从余数中减去调整的分母并将结果存在余数寄存器中，如果新的余数为正，我们就将商加1，否则商不变并且还需要通过加上分母来还原从前的余数值。我们可以采用状态机的设计结构来实现该种除法算法思想。

本项目中Restoring算法主要应用于：幅度衰减模块中除法器的设计。

2.4 分段函数算法简介

分段函数是对于自变量不同的取值范围，有着不同的对应法则的函数。对于分段函数的实现具有资源消耗少，处理速度快的特点。例如，一种包含二阶非线性函数的分段函数，如下式所示：

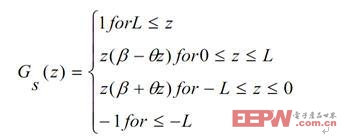
对于二阶非线性函数的实现，如图15 所示：

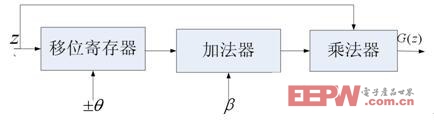
图15 二阶非线性函数的实现

本项目中分段函数主要应用于：人工神经网络中的激活函数的

f（n）的设计。

3. 项目设计细化模块方案

项目设计细化模块的框图，如图16所示：

本次项目的设计难点：

（1）准确测定延时信息的自相关模块的设计，因为自相关信息会对收发信号的幅度提取有着很大的影响。

（2）高效的64阶滤波器的设计，旨在设计一种既节省硬件资源又能高效实时输出的一种低通滤波器。

（3）可准确分类的人工神经网络的设计，需要大量的离散学习和确定一种准确的拓扑结构。

图16 项目设计细化模块框图

推荐阅读：30例经典检测、监测、监控系统完整解决方案，从实际应用需求出发