海底管道检测信标设备水下运动状态研究
摘要:本文根据重力选矿、流体力学、大学物理等知识并参考鱼雷入水文献,分析推导并修正了阻力通式,研究了海底管道检测信标设备的水下运动状态和相同当量直径的球体在水下的运动状态。通过MATLAB仿真得到时间、速度和位移关系曲线。最终在山东烟台海试测得的实验数据验证了理论分析的可靠性。创新之处在于将物理选矿中的李莱曲线应用于信标运动状态的分析研究。
引言
近年来,由于海洋防务和开发的需求,水下遥控技术越来越受重视。目前来看,在海水中传递信息、无线电波和光很容易被吸收并形成散射,而声波在海洋中的传播速度约为1530m/s,远远大于在空气中的340m/s的速度,并且衰减很小。所以声波是目前水中信息传输的主要载体,水声通信成为水下遥控信息传输的主要手段。
海底管道检测信标设备(以下简称信标)应用水声通信的调制解调和编码解码技术对海底管道进行漏磁检测,以防管道因年久失修或腐蚀而出现故障。
信标通常用于水下300m以内的浅海领域的石油管道故障检测。故信标由静止状态从水面下降到水底过程的研究和从水下解锁上浮到水面过程的研究对于信标测试具有实际价值。运动状态的分析、计算、仿真和实验对于确定信标设备的最佳材质和尺寸以及水下的实际布放具有指导意义。
1 球体水下运动状态研究
信标设备的形状与球形物体有相似之处。在分析信标设备的运动状态前,分析和研究相同材质和体积等参数的球体在水下的运动状态是很有必要和价值的。通过修正球体运动的阻力通式即可得到信标运动所受阻力的通式。
1.1 球体水下受力分析
球体由静止状态从水面下降到水底的过程如图1所示,初速度、初加速度和初始位移均为0。
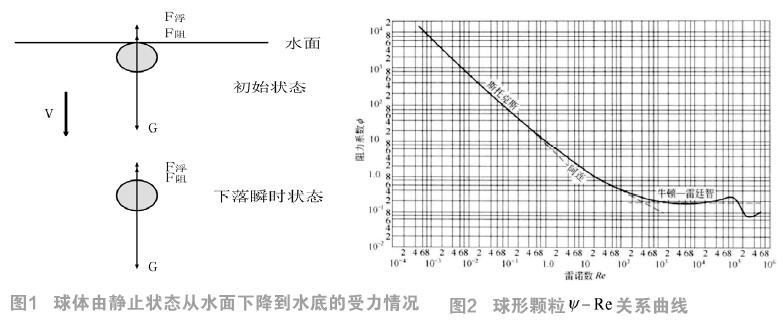
忽略流体相对地面的运动,球体下落过程做的是变加速直线运动。球体水下主要受力为重力、浮力和阻力。重力和浮力为恒定值,球体阻力随速度的增大而增大。当达到一定速度时,球体处于平衡状态,保持匀速直线运动继续下降,直到水底。信标设备放置区域为200m以内的浅海领域,故分析0m~300m位移内球体的运动。
根据牛顿第二定律得到运动方程:
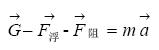 (1)
(1)
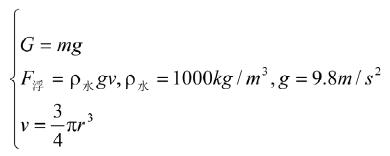
雷廷智根据牛顿理论推导出球体在理想流体中运动的阻力公式,后经修正得到湍流条件下的压差阻力公式:
 (2)
(2)
上式适用于雷诺数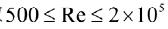 ,此时阻力与速度的平方成正比。
,此时阻力与速度的平方成正比。
Re≤1时,阻力为粘滞阻力,应用斯托克斯公式,阻力与速度成正比。
当物体运动的雷诺数在牛顿-雷廷智公式与斯托克斯公式之间,即1≤Re≤500,两种阻力同时影响物体的运动。阿连曾在实验基础上提出一个适合2≤Re≤300的阻力公式[1]:
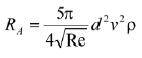 (3)
(3)
量纲分析原理中的π定理内容:对于某个物理现象,如果存在n个变量互为函数关系,即:
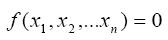 (4)
(4)
其中有m个为基本量(量纲独立),则该物理现象可以由(n-m)个无量纲项所表达的关系式来描述。即:
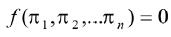 (5)
(5)
式中, 为(n-m)个无量纲数[2]。根据量π定理可以求得球体绕流运动的阻力通式如下:
为(n-m)个无量纲数[2]。根据量π定理可以求得球体绕流运动的阻力通式如下:
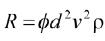 (6)
(6)
其中Φ为阻力系数,是雷诺数的函数,即f=f(Re)。英国物理学家李莱用实验方法确定了Φ-Re关系曲线[3]如图2所示。曲线的纵坐标与横坐标均用对数表示。可以看出,Φ随Re的增大而连续平滑地减小。已知Re可以估算出阻力系数。
1) Re≤1时,斯托克斯公式成立,主要考虑粘滞阻力,流体处于层流状态,阻力与速度成正比;
2) 500≤Re≤2≤105时,牛顿-雷廷智公式成立,主要考虑压差阻力,流体处于紊流状态,阻力与速度的平方成正比;
3) 2≤Re≤300时,阿连公式成立,两种力并存,雷诺数不同,两种力的比例不同,流体处于过度状态。
1.2 球体阻力的修正
考虑信标的当量直径很大,故达到沉降末速时的雷诺数可高达李莱曲线的末端,故要推测出超出牛顿-雷廷智公式区域外的阻力系数,而不能仅仅采用固定的阻力系数。根据李莱曲线修正后的阻力系数与雷诺数的关系如下:
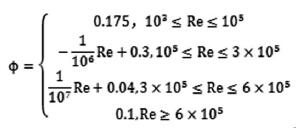 (7)
(7)
由于Re是速度和直径的函数,故直径确定下,可分段求解二阶微分方程,确定每段的初始条件,最后利用MATLAB求解微分方程,得到运动关系曲线。这种修正阻力系数的方法使阻力系数的确定更加精确,进而仿真结果更加可信,适用于高雷诺数下阻力的计算。
1.3 球体MATLAB仿真结果
研究球体在水下的运动过程,方程如下:
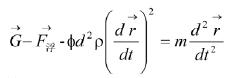 (8)
(8)
整理得:
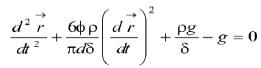 (9)
(9)
由于球体下落过程的雷诺数很大,故球体运动过程主要是在紊流区域,符合牛-雷公式,阻力系数为定值。
MATLAB仿真,将高阶微分方程转化为一阶微分方程组,即状态方程,然后基于龙格-库塔法求解此方程组,得到二阶微分方程满足初始条件下的特解。龙格-库塔法的一般调用格式为:
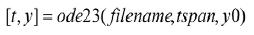 (10)
(10)
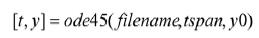 (11)
(11)
其中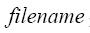 是定义
是定义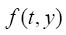 的函数文件名,该函数必须返回一个列向量。tSPAN形式为
的函数文件名,该函数必须返回一个列向量。tSPAN形式为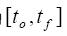 ,表示求解区间, y0是初始状态列向量,t和y分别给出时间向量和相应的状态向量。这两个函数分别采用了二阶、三阶、四阶和五阶龙格-库塔法,并采用自适应和变步长的求解方法,即当解的变化较慢时采用较大的步长,从而使得计算速度很快;当解的变化较快时步长会自动变小,从而提高计算精度[4]。
,表示求解区间, y0是初始状态列向量,t和y分别给出时间向量和相应的状态向量。这两个函数分别采用了二阶、三阶、四阶和五阶龙格-库塔法,并采用自适应和变步长的求解方法,即当解的变化较慢时采用较大的步长,从而使得计算速度很快;当解的变化较快时步长会自动变小,从而提高计算精度[4]。
信标设备 阻力通式 李莱曲线 沉降末速 运动状态 201606 相关文章:
- DIY一款具运动状态追踪功能的遥控玩具,做守护天使(04-17)
- 高速微型光电检测电路设计(05-26)
- 信标组裁判系统原理与实现(05-26)
- 频宽、取样速率及奈奎斯特定理(09-14)
- 为什么要进行信号调理?(09-30)
- IEEE802.16-2004 WiMAX物理层操作和测量(09-16)
