运算放大器电路固有噪声的分析与测量之放大器的内部噪声（1）

本文将讨论决定运算放大器 (op amp) 固有噪声的基本物理关系。集成电路设计人员在噪声和其他运算放大器参数之间进行了一些性能折衷的设计，而电路板和系统级设计人员将从中得到一些启发。另外，工程师们还能了解到，如何根据产品说明书的典型规范在室温及超过室温时估算最坏情况下的噪声。

　　最坏情况下的噪声分析和设计的 5 条经验法则

大多数运算放大器产品说明书列出的仅仅是一个运算放大器噪声的典型值，没有任何关于噪声温度漂移的信息。电路板和系统级设计人员希望能根据典型值找出一种可以估算最大噪声的方法，此外，这种方法应该还可以有效地估算出随着温度变化的噪声漂移。这里给出了一些有助于进行这些估算的基本的晶体管噪声关系。但是为了能准确地利用这些关系，我们有必要对内部拓扑结构（如偏置结构和晶体管类型等等）进行一些了解。不过，如果我们考虑到最坏情况下的结构，也可以做一些包括大多数结构类型的概略性说明。本节总结了最坏情况下的噪声分析和设计的 5 条经验法则。下一节给出了与这些经验法则相关的详细数学计算方法。

经验法则 1：对半导体工艺进行一些改变，不会影响到宽带电压噪声。这是因为运算放大器的噪声通常是由运算放大器偏置电流引起的。一般说来，从一个器件到另一个器件的偏置电流是相对恒定的。在一些设计中的噪声主要来自输入 ESD 保护电阻的热噪声。这样的话，宽带噪声的变化超过典型值的 10% 是非常不可能的。事实上，许多低噪声器件的这种变化一般都低于 10%。请参见图 7.1 示例。

宽带电流噪声要比电压噪声更容易受影响（主要是对双极工艺而言）。这是因为电流噪声与基极电流密切相关，而基极电流又取决于晶体管电流增益 (beta)。通常来说，宽带电流噪声频谱密度的变化不到 30%。

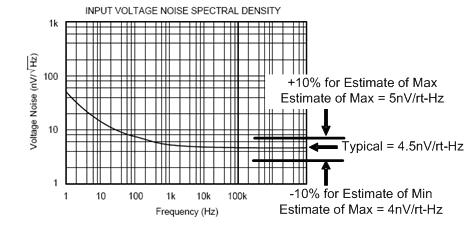
图 7.1 基于典型值估算的室温条件下的宽带噪声

经验法则 2：放大器噪声会随着温度变化而变化。对于许多偏置方案 (bias scheme) 来说（如，与绝对温度成正比的方案，PTAT），噪声以绝对温度的平方根成正比地增大，因此在大范围的工业温度内噪声的变化相对很小（如，在 25℃ 至 125 ℃之间仅发生 15% 的变化）。但是，一些偏置方案（如，Zero-TC）可以产生与绝对温度成正比的噪声。对于这种最坏情况而言，在同一温度范围内噪声变化为 33%，请参见图 7.2 图解。

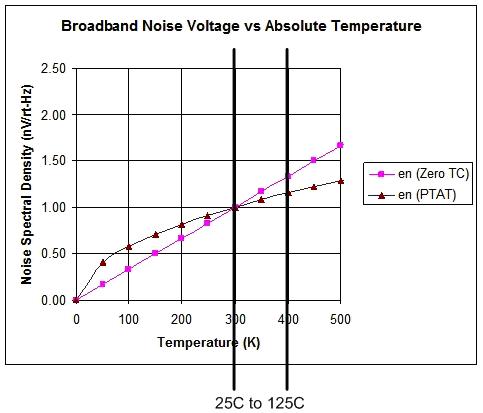
图 7.2 噪声在最坏情况下和典型情况下的变化与温度的关系

　　经验法则 3：1/f 噪声（如，闪烁噪声）极易受工艺影响。这是因为晶体结构制造工艺过程中会产生一些瑕疵，1/f 噪声的产生则与这些瑕疵有关。因此，只要半导体工艺得到很好的控制，那么 1/f 噪声就不会出现较大的漂移。制造或工艺变化都会给 1/f 噪声带来巨大的变化。大多数情况下器件产品说明书都给出了 1/f 噪声的最大值，却没有提及工艺或最终测试时对器件进行的测量。如果产品说明书没有给出 1/f 噪声的最大值，那么，假定在并没有对工艺控制进行优化来减少 1/f 噪声的情况下，三种变化因素可用来估算最坏情况下的噪声，请参见图 7.3。

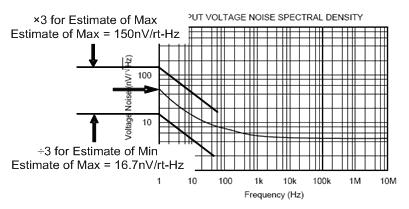
图 7.3：最坏情况下的 1/f 噪声估算

经验法则 4：电路板和系统级设计人员需要了解的一点是，Iq 和宽带噪声呈负相关。严格来说，噪声与运算放大器输入差动级的偏置相关。但是，由于这类信息还没有正式公布过，所以我们可以假定 Iq 与差动级偏置成正比。对于低噪声放大器来说，这个假设是成立的。

一般说来，宽带噪声与 Iq 的平方根成反比。但是，对于不同的偏置方案这个反比关系也会发生变化。此条经验法则有助于电路板和系统级设计人员更好地了解 Iq 和噪声之间的折衷方法。例如，设计人员不应该指望放大器带有极低的静电流，进而产生低噪声。图 7.4 图解说明了该关系。

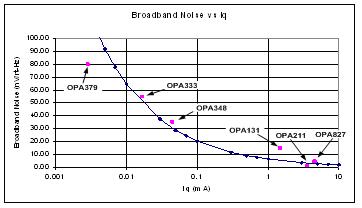
图 7.4：Iq 与宽带噪声的关系

经验法则 5：FET 运算放大器固有电流噪声非常低。这也说明了双极与 FET 晶体管以及噪声之间的差异。因为 FET 放大器的输入栅极电流比双极放大器的输入基极电流小得多。相反，在给定一个偏置电流值（如，输入级的集电极电流或漏极电流）的情况下，双极放大器具有更低的电压噪声，请参见图 7.5 的多个示例。

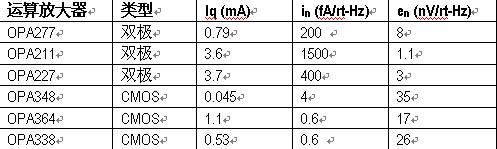
图 7.5 MOS 放大器与双极放大器的电压及电流噪声的对比

　　双极噪声的详细数学计算方法

图 7.6 表明了双极晶体管噪声模型的原理。图 7.7（方程式 1、2 和 3）中给出了双极晶体管的基本噪声关系。在该部分中，我们将利用这些方程式，以得出一些基本关系，而经验法则就是基于这些基本关系得出的。

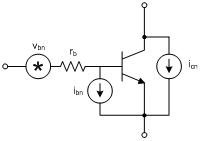
图 7.6 双极晶体管噪声模型

图 7.7 双极噪声基本关系

　　利用方程式 1 进行分析：双极热噪声

方程式 1 说明