内建式抖动测量技术（下）

模拟结果

《图十六 动放大电路之转移曲线图》

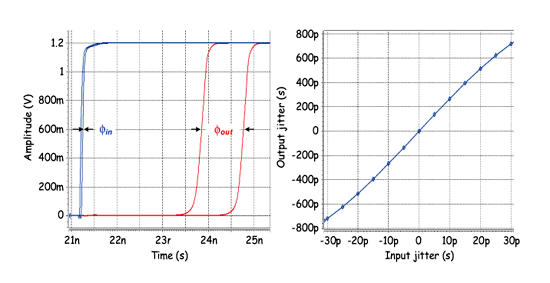
（X轴：输入抖动量；Y轴：输出抖动量）

内建抖动测试架构中最重要的元件为抖动放大电路，因为其放大倍率将影响系统解析度以及稳定度，所以首要工作就是确保抖动放大电路操作特性。如图十六即为抖动放大电路之模拟结果。当时脉抖动产生时，经由此电路可把时脉边缘扯开，也就是增加相位误差量。另外我们可利用不同输入抖动量来观测抖动放大电路之操作线性度，如图十七所示。若所模拟出来的转移曲线呈现相同斜率，代表此电路的放大倍率为一定值；但若曲线呈现出许多斜率，则可明显观察出放大倍率于不同输入抖动时具有不同的放大倍率，所以我们便需针对制程漂移对电路影响作模拟分析。

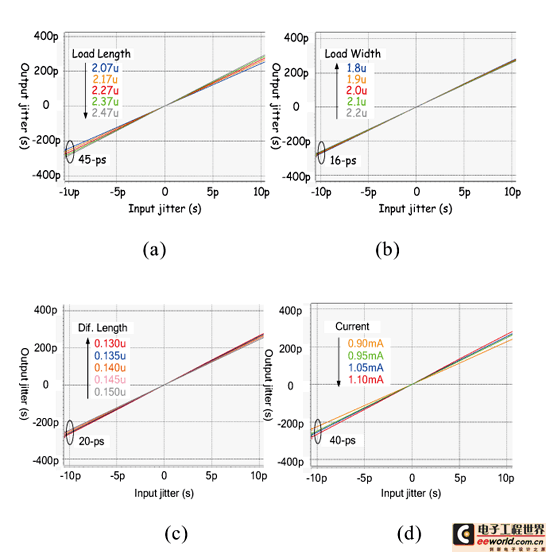
《图十七 放大倍率vs.制程漂移：（a）Load length；（b）Load width；（c）Diff. pair length；（d）Bias current》


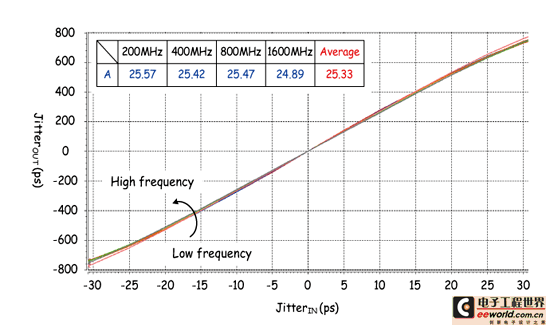
《图十八 放大倍率 vs. 操作频率》


抖动放大电路分析结果

先前介绍过抖动放大电路是藉由电流充放电速度来达到抖动放大，因此负载以及电容量将决定抖动放大的程度，所以以下就针对四个关键点作分析，并模拟其转移曲线图。由图十七所示，（a）～（d）分别为负载电晶体之length、负载电晶体之width、差动对电晶体之length和偏压电流变异时之模拟。从中可以观察出放大倍几乎皆维持在固定的倍率，但在负载电容（length）与操作电流变化时对于系统有较大的偏移量，约40-ps。

不过以整体系统来看，因为采用的是放大抖动量来测试，再将结果除以倍率得到原始抖动量，所以虽然模拟看出放大后的抖动约有40-ps的变异，但除以放大倍率25以后其变异约为1.6-ps，此误差量对于整体测试值几乎可忽略不计。此外，图十八为抖动放大电路操作于不同频段的转移曲线图。从中可明显发现，不论是在低频或是高频操作时，其皆具有近似的transfer curve，所以即验证此抖动放大电路具有宽操作范围以及线性抖动量放大之特性。因此由以上模拟可知，我们所提出之抖动放大架构将可运用在抖动测试系统中。

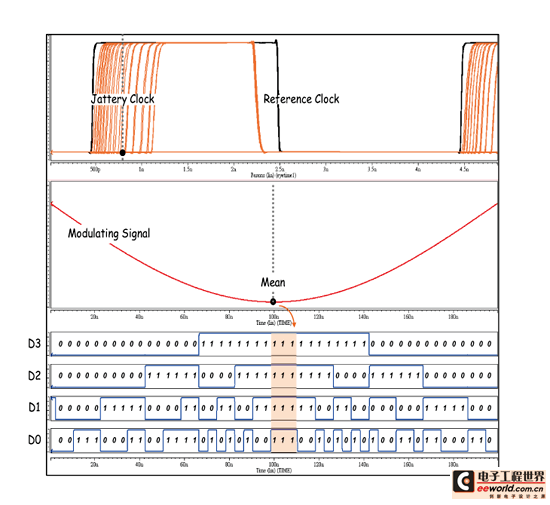
《图十九 模拟验证用之抖动产生示意图》


周期对周期抖动系统观察

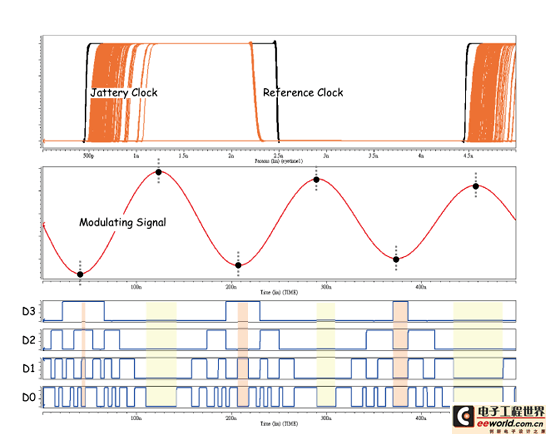
为了确保整体系统操作正确性，接着我们将实际输入周期对周期抖动至系统中，藉此观察其操作特性。而周期对周期抖动的产生方式，我们将采用讯号调变法来实现，如图十九所示。其包含一个干净的参考时脉（input signal）、一个作为干扰源的调变讯号（modulating signal）和相位调变电路（phase modulator），藉由杂讯去改变理想时脉转态点实现抖动产生。

而以电路面来看，其实相位调变电路就是可调整电源电压的多级缓冲器。当一理想时脉进入缓冲器后，会有延迟产生，而延迟量和电源电压有极大关连性。电压越大延迟越小；反之电压越小延迟就会越大。利用此关系，我们只要将抖动做为缓冲器电压，就可以得到随着抖动变化的时脉相位。

抖动数位化观察

为了验证此系统是否能正确地把输入抖动数位化，因此我们也将利用两种不同型态之抖动来验证：一为正弦抖动、另一为振幅调变抖动。如图二十和二十一所示的抖动量数位化之模拟结果。从中可以得知，相关系统可成功依输入抖动型态运算出对应数位码，我们只需将数位码对照抖动表，即可得知输入抖动量。

《图二十 正弦抖动经抖动测试系统之输出结果》


《图二十一 调幅抖动经抖动测试系统之输出结果》


抖动测试准确度和测试时间关联密切，在足够测试样本下才能确保所得数值具备公信力，在测试时就必须让系统做长时间累计。我们将测试前述两种型态之抖动分布，此时系统会送出许多测试数值；而为了得知其真实抖动分布的情况，因此我们累加所有抖动量分布次数，其测试结果如图二十二所示。

抖动数值对应分析

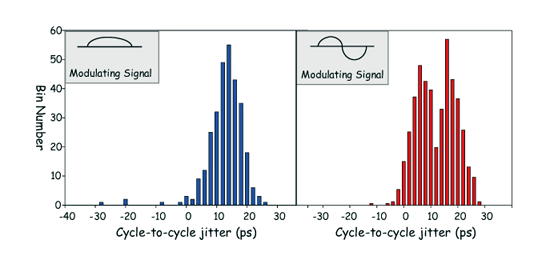
经过长时间运算后，在半周期正弦抖动部份，图二十二左明显可看出其为一高斯分布，具有一个峰值，此值就落于正弦抖动的最大值上。而右图振幅调变抖动之测试结果，则显示双峰之抖动分布，且其双峰的分布量也不尽相同。这是因为振幅调变讯号每个峰值电压不同，而不同的峰值会对应到不同的数位码，所以在长时间抖动测试下才会出现此分布情形。

藉由以上的说明可得知，我们所提出之抖动测系统不但可以成功量化抖动量，并可藉由长时间的分析，可进一步地得知抖动分布型态，更可从中运算出抖动峰值、抖动均方根植、n倍sigma的抖动分布量…等等。

《图二十二 长时间累计抖动运算结果》

所提出测试法之测试结果

《图二十三 抖动产生示意图与实际测试图》


利用宽频抖动测试讯号

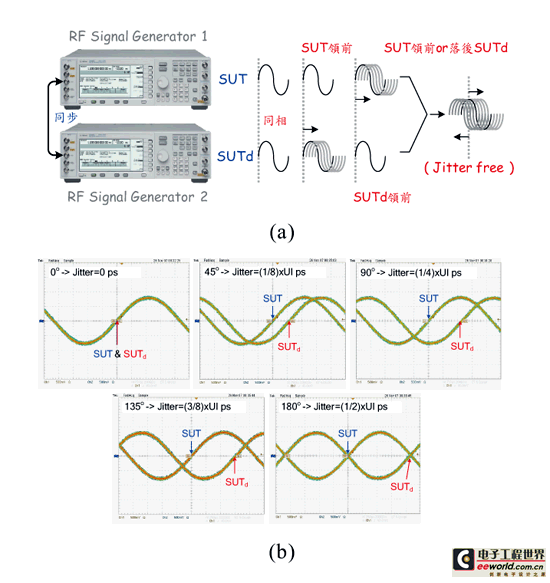
在量测环境的建构上，我们可分为两个部份：一为针对抖动放大电路作测试，另一则为全系统测试。在先前架构说明中提到，我们所提出的测试架构是针对待测讯号之周期对周期抖动作测试，因此需要一延迟电路，将每个周期讯号与延迟一个周期时间之讯号萃取出来。但为了要验证抖动放大电路操作特性，我们也需要一非常宽频与宽范围抖动测试讯号，因此采用图二十三的测试法。

亦即我们利用两台高频讯号产生器，分别产生代表SUT与SUTd之待测时脉讯号，因为时脉已强制同步，所以若不改变任何参数时，SUT与SUTd之讯号将保持同相位。而为了测试抖动放大电路的放大特性，可藉由调整其中一台讯号产生器之延迟量，来仿造实际时脉抖动情形。

如图中可以观察出，若调整讯号产生器2的延迟量，可实现落后抖动分量；若调整讯号产生器1的延迟量，则可实现领前抖动分量，藉此调整将可达到宽抖动范围之测试。此外因讯号产生器可产生大范围频率调整，所以也可进一步测试抖动放大器线性度。

《图二十四 抖动放大电路量测环境示意图》


分析测试过程

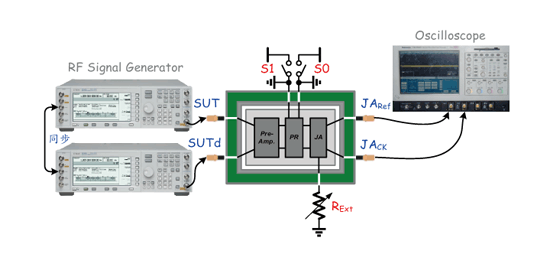
图二十四为抖动放大电路测试环境示意图，其输入讯号为前述两台讯号产生器所提供之讯号。于晶片中前端会先有预先放大器（pre-amplifier）将输入转换为方波，随之送入脉波吞噬电路与抖动放大电路中。当抖动量经电路放大后，我们利用示波器来观测输出讯号间的相位差，再将输出相位差（JACK-JARef）除以输入相位差（SUT-SUTd），即可得到抖动放大电路之放大倍率。

此外当输入讯号频率改变时，可藉由调整S1和S0来选择较为适当的脉波吞噬数；而若当抖动放大电路于制作时发生漂移，则可藉由调整外部电阻RExt进而改变电流量，以确保抖动放大量的准确性。因此由以上所述之方法，将可测试出抖动放大倍率之线性度（JitterIn vs. JitterOut）、操作频宽（频率 vs. 放大倍率）与放大倍率和脉波吞噬数间的关系。

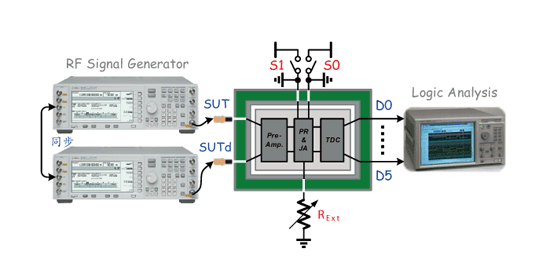
《图二十五 抖动量测系统之量测环境示意图》


抖动量测环境分析过程

另外图二十五为抖动量测试系统之量测环境示意图。其前端和图二十四做法一致，但因抖动放大电路后接上时间-数位转换电路，因此已将抖动量化成数位码，所以我们藉由逻辑分析仪（Logic Analysis；LA）来运算即时输出之数位码；经一段有效时间运算后，再把逻辑分析仪所输出之结果与输入抖动量相比较，即可得知所提出之系统准确度。

《图二十六 输入抖动与输出抖动之量测图：随着箭头方向代表输入抖动递增》


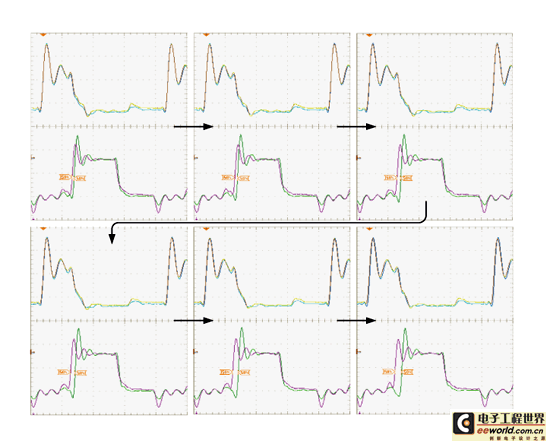
首先，我们将所提出的抖动放大电路，使其操作在不同输入抖动量下，观察放大倍率间的变化，如图二十六所示。为了测试纪录方便，我们采用6个测试pattern来验证，也就是说利用6个不同的输入抖动量送入抖动放大电路中，然后量测输出抖动量，以绘出抖动放大曲线图。此外为了验证我们所提出的脉波吞噬观念可修正放大线性度，所以也针对四个频段做验证。

《图二十七 抖动放大倍率vs.操作频率》


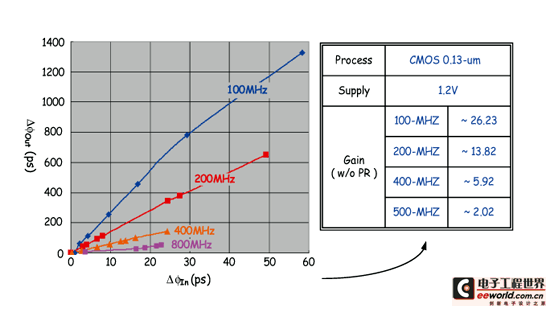
抖动放大电路测试结果

图二十七即为抖动放大电路测试结果。从图中可观察出，在低频操作时，因为稳态区域足够，所以其输出抖动与输入抖动比，与当初所设计的相距不远。但随着待测讯号频率上升、稳态区间缩小，在不调整脉波吞噬数目的条件下，放大倍率会随之缩小，甚至放大倍率消失，导致系统操作错误。以800-MHz的条件为例，此区段放大倍率已下降至约2倍左右，此时已完全无法弥补时间-数位转换电路解析度不足的缺点。因此从此测试可观察出，虽于各频段内放大倍率皆可维持放大倍固定，但只要输入讯号频率一变化，就会造成放大倍率失真以至于会有误判的情形。因此接下来将依前述的说明适当切换脉波吞噬数，来达到宽频之放大倍率。

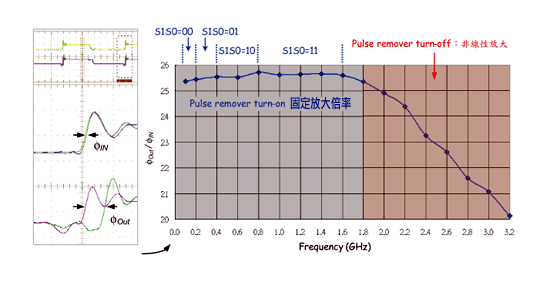
如图二十八所示，在不同频段操作下我们去改变脉波吞噬的数目，也就是切换S0、S1，让抖动放大电路在不同频段下皆具有足够宽的稳态区间。此外也藉由调整外调电阻将抖动电路之放大倍率作些微的修正。图中显示经调整脉波吞噬数后，于数十MHz～1.6GHz附近其放大倍几乎维持在25.5倍左右。但若超过1.6GHz后，因为tfn时间点慢慢靠近ts造成稳态电位的变化，所以放大倍率开始有些许改变。操作频率继续往上升，tfn点会等于或是超前ts，造成放大倍率急速下降，所以说此抖动放大电路的线性放大区为数十MHz~1.6GHz。在此必须说明因为线性区间可藉由改变脉波吞噬的数目来达成，因此若须操作在更高频的运用上时，我们只需依造（2）式来实现即可。

《图二十八 放大倍率与频率间之关系图》


《图二十九 多工式振荡器之振荡频率测试图》


时间-数位电路最佳解析度

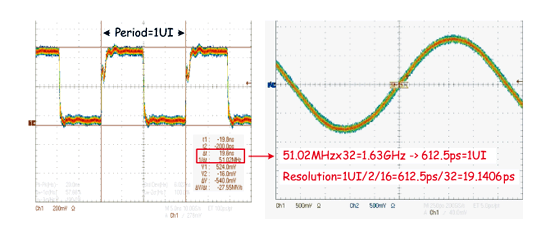
除了抖动放大电路测试外，时间-数位转换电路也关系到系统最佳解析度。因此也藉由调整输入抖动量来观察数位输出码，并测试多工式振荡器振荡频率来回推解析度。如图二十九所示，为了测试方便，我们将振荡频率除以32来观测，所以此时间-数位转换电路的最佳解析度，为振荡周期除上32个相位（经内插后所得），亦即约为19-ps。

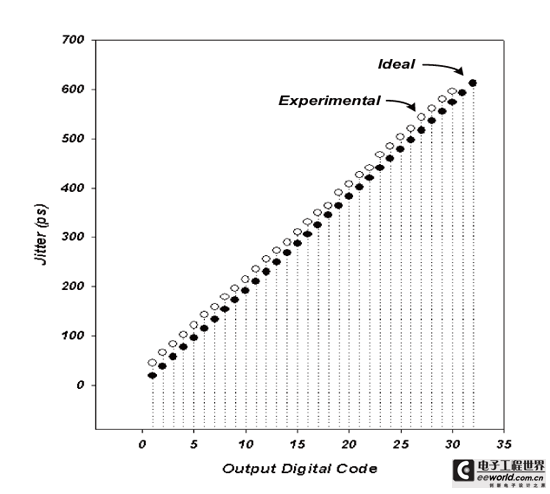
此外图三十为输入抖动量与数位输出码之对照图。其显示输入抖动每增加19-ps数位码也随之增加，但量测曲线与理想曲线间相差约40-ps。此误差量来自于振荡器之抖动。但以系统层面来看，我们只要将此误差量扣除即可，因为其所关心的是每个数位码间所代表的抖动量是否相同，因此我们将图三十误差量归零后进行积分非线性误差量（Integral Nonlinearity；INL）之分析，如图三十一所示。此时间-数位转换电路最大偏移量约为6-ps，即0.32LSB（1LSB=19-ps），其小于0.5LSB，所以可说对于系统操作时并不会带来严重的错误。

《图三十 输入抖动 vs. 数位输出码》


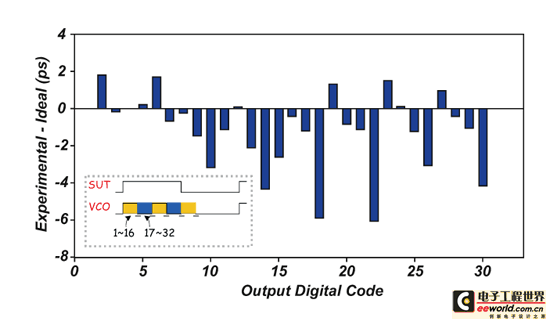
《图三十一 时间数位转换器之INL分析图》


得出系统解析度

确定了抖动放大电路与时间-数位转换电路操作特性后，接着我们将可推得系统解析度。因为放大倍率A与延迟单元之延迟时间的比例为25.5:19，所以在此条件下所能测到的最佳解析度即为19-ps/25.5=0.8-ps。同理可证，若在设计上将倍率提升或是缩小延迟时间至其比例为1:2时，此将可把解析度进一步提升至0.5-ps。有鉴以上量测与模拟之结果，我们可以说此测试方法将可成功运用在wide range以及low jitter的内建时脉抖动测试架构中。

结语

在先前所列举的五种传统测试架构，不外乎是利用电路技巧来缩小延迟单元的延迟时间，以等效增加测试解析度。然而当测试速度上升或是抖动量来到sub-ps等级后，因电路与制程上之瓶颈，其所能量测的范围皆会受到限制。

基于上述之原因，本文提出不同于传统测试架构的测试策略。这是采用抖动放大的观念，先针对待测讯号抖动量做先期放大，然后利用时间-数位转换电路将抖动量化，再把得到的输出数位码除以放大倍率，即可还原出原本的周期对周期抖动量。此外为了让此测试架构能操作在任何频段下，因此还采用单撷取搭配脉波吞噬的测试方法，拉长抖动放大时的稳态时间，以得到固定放大倍率，进而减少因频率变化所带来的量测误差。所以本文所提出方法相较于传统测试方式，将具备宽频操作、低抖动量测试、高解析度、成本低、受测试环境限制程度小等优点。最后其比较如表三所示。

(表三) 各种架构比较表