内建式抖动测量技术(中)
时间:01-09
来源:互联网
点击:
抖动放大电路设计架构 [7] [8]
《图九 抖动放大电路之架构图与时序图》
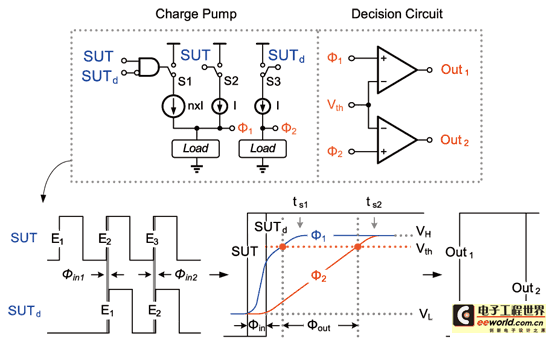
周期对周期抖动量即为后一个周期边缘En+1和前一个周期边缘En之相位误差,因此若要实现抖动量放大就必需将En和En+1间之边缘时间差拉大。在本文中将采用电流对负载充放电之原理来达到抖动放大之功能。我们以图九来说明其操作原理。
抖动放大电路基本上是由两组不同电流量之电荷帮浦(Charge Pump;CP)与决策电路(Decision Circuit;DC)所组成,而分别由待测讯号SUT、一个周期延迟后之讯号SUTd与两者之组合来控制。其最基本的想法为利用不同充电斜率(即充电速度)搭配讯号不同起始点(即转态边缘)之特性,来合成出具有较大抖动量的时脉边缘。而为了清楚解释其放大原理,我们将SUT(S)与SUTd((Sd)依相位关系区分成四个区间,然后分别探讨在不同区间内的操作情形。如表一所示。
(表一) 电荷帮浦操作状态表


搭配图九与表一之叙述,从中可以得知在初始状态时因SUT与SUTd为低电位,开关皆turn off,所以并无任何电流对负载做充电因此输出结果(f1、f2)将为低电位(VL)。但若当两个phase间有抖动存在时,SUT会为高电位而SUTd为低电位。此时f1会以(n+1)倍的电流对负载充电pull up,而f2因S3 turn off所以将保持前一状态的低电位。接着经过Δτ的时间后,SUTd也pull high,促使S3 turn on、S1 turn off,此时f1和f2将一起以I的速度往高电位移动。但是仔细观察Region II和Region III之过程,因在Δτ的这段时间里f1先以较快的速度启动,若Region III在相同充电的斜率条件下(电流量皆为I)其会先到达稳态位准;而接着再经过n*Δτ时间后,f2才也会到达此位准。此时从图九中可以看出f1、f2与所设定的临界电压(Vth)有两个交点,若用两组决策电路将转态点判断出来即可产生两组不同相位差的输出讯号(Out1、Out2)。所以利用上述之条件,我们可以简单以公式一来表示出输出与输入间的关系:
《公式一》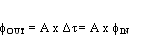
其中fOUT为Out1、Out2间的相位差(放大后之周期对周期抖动量)、fIN为SUT、SUTd间的相位差(放大前之周期对周期抖动量),而A即代表放大倍率。
利用上述概念,本创作即可将时脉讯号之周期对周期抖动量加以放大,来弥补时间-数位转换电路的不足。然而单纯光靠电流充电能力的行为模式来达成放大目的,会面临电路操作瓶颈进而导致测试误差产生,例如放大倍率的非线性或是操作频率变化等,接下来我们会针对这些效应提出解决之道。
抖动放大电路及Pulse Remover设计的分析
(表二) 符号表示

在抖动放大电路基本设计中,因为是使用电流对负载充放电之速率来达到抖动放大,因此先针对充放电位准以及时间作定义。如表二所示。
图十(a)中,通常抖动放大电路在低速率操作时,因其抖动量相较于半个周期时间所占的比例较小,因此电荷帮浦输出(f1、f2)到达高稳态点时间(ts1、ts2)通常会小于负缘转态点时间tf。
《图十 抖动放大电路时序图:(a)Case 1 : tf>ts2;(b)Case 2 : tf≈ts2;(c)Case 3 : tf

所以在此频段操作因有足够的稳态区间(stable region),其经决策电路后产生之输出相位差fOUT相较于输入相位差fIN几乎能维持定值,也就代表放大倍率A为constant。但若当待测时脉频率上升后,如图十(b)所示,随着讯号周期缩短tf之发生点提前,在tf非常接近但大于ts2时,抖动放大电路依然可勉强维持住放大倍率,所以此时即称为操作临界值。但假若不幸在所使用的应用中tf发生较大的变异或是操作频率继续往上升,导致ts2比tf晚发生,则放大倍率将开始产生非线性的变化。
从图十(c)可观察出在正常的操作模式下f1与f2最后皆会回到稳态位准VH、VL。但假若转态边缘tf在尚未稳定前就出现,则f1与f2之电压会被强制维持在新的位准上,也就是VH’(=VH-ΔV)与VL’(= VL +ΔV)。这个现象虽对于第一个周期(initial stage)之放大倍率没有造成影响,但是从图中得知,在下一个周期(next stage)中因为f1、f2电压起始位准点有了变化,所以经充电后与临界电压Vth的交点必然随之改变。换句话说就是voltage domain variation将转换成time domain之phase error,此时即会造成放大倍率变动。因此周期对周期抖动放大电路需操作在wide range之应用时,就必需利用一些机制控制稳态时间点ts比负缘转态点 tf早发生,如此才不会造成放大倍率的失真。有鉴于此,本文将提出一个使用脉波吞噬观念之单撷取量测方式来改善之。
脉波吞噬之单撷取量测方式
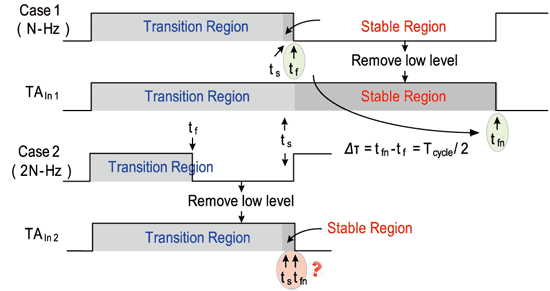
《图十一 脉波吞噬概念图》
以上述讨论可知,若要实现tsf,不外乎是将稳态时间点往前拉会或者是延迟负缘转态点产生之时间。以电路实现角度而言,因ts是电流对负载充电后所产生的电压与高电位VH之交集,所以电流越大、回到稳态点能力越强,相对其出现时间会越早。但抖动放大的产生就是藉由不同速率电流之差所得,想必然放大倍率也将受到影响。所以为了兼顾放大倍率与电流量间trade-off,本文将采用延迟tf之作法来维持不同操作频率下的抖动放大倍率。
如图十一case1所示为一低频操作时的示意图。为了让抖动放大电路的放大倍率维持定值,待测讯号的ts必需小于tf,而worst case会发生在ts等于tf的时间点,此时稳态区间几乎会近似于零,也就是说放大倍率会非常不稳定。
为了改善这个问题,以先前的说法就必需将tf时间点做延迟。简单来看就是把测试速度放慢,利用脉波吞噬电路移除掉0.5个周期,来换取稳态区间之宽度。如图所示,若把case1的讯号做处理后成为TAIn1,其负缘转态时间点发生的时间往后延迟了Δτ(=tfn-tf=Tcycle/2),这代表着稳态区间随之放大2倍。因此若把待测讯号的频率增加后,其因具有足够的稳态时间,所以放大倍率将不受到clock variation和频率变动之影响。
但在图十一 Case2中,待测时脉讯号操作速度持续上升(约为Case1的两倍),可以很明显观察到若不采用脉波吞噬机制,ts已远远超越了tf,此时抖动放大电路之放大倍率已为非线性操作;但若加入脉波吞噬的机制后,因待测讯号速度太快,在相同充放电的速率条件下,ts也非常靠近tfn,放大倍率变异的问题还是存在。所以由此可知真正要达到wide range的操作,不管在任何频率下,皆需要拥有相同的稳态区间,才会真正得到constant之放大倍率。有鉴于此,我们将脉波吞噬的机制稍做修改,将不再维持固定移除0.5个周期,而是随着待测物的频率每增加一倍而随之变化,其remove number可由公式二表示之:
《公式二》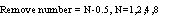
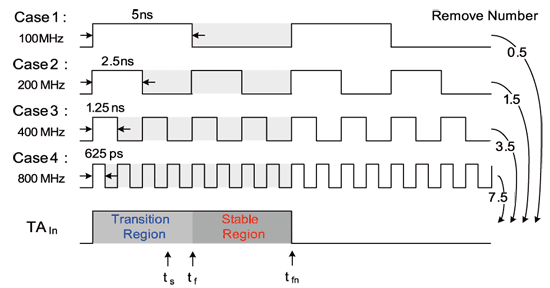
其中N为频率变化率。在本文中所提出的例子因为要达到数十MHz~1.6GHz之操作,所以将100MHz定为基准,频率每增加一倍就必需改变remove number来维持放大倍率。如图十二所示。
《图十二 于各操作频段间之脉波吞噬概念图》
以电路的角度而言,要实现图十二脉波吞噬电路其实不难,只要将待测讯号依频段经过相对应的除频器即可实现。但实际上若直接把待测讯号经过除频器来达到脉波吞噬,依参考文献[9]之说法,该讯号的抖动也同时间会被放大,约为 √n倍。此外,除16的电路最少需要4组DFF来实现,代表待测讯号到达抖动放大电路前就必需经过许多transistor,进而受到power noise或是thermal noise干扰导致抖动上升,这将会严重影响量测准确度。
以边缘检测达到脉波吞噬效果
《图十三 (a)所提出之抖动放大电路;(b)边缘检测电路操作示意图》
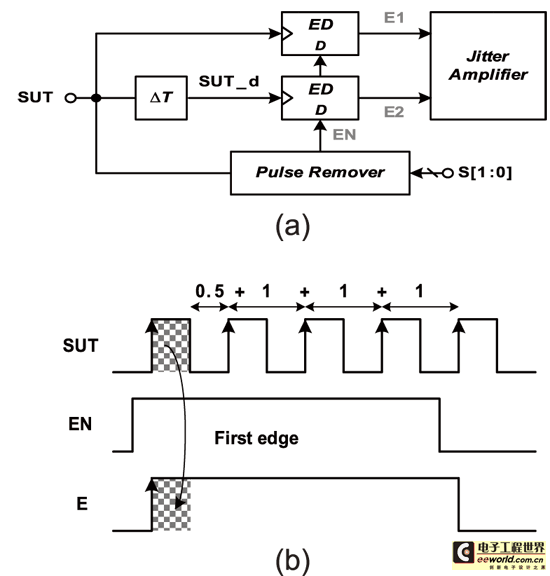
因此本文将采用边缘检测(edge detection)之技术来达到脉波吞噬的效果,如图十三(a)所示。其主要包含两大方块:边缘检测器与脉波吞噬电路。首先,当待测讯号启动后,为了维持放大倍率,需先进行pulse remove的动作。以图十三(b)为例,SUT为待测讯号,EN为脉波吞噬电路所产生,E为经过处理后的待测讯号。其中脉波吞噬电路是由MUX所实现,其可藉由控制s脚位来选择EN讯号为SUT之/2、/4、/8、/16的结果。
此外EN接至边缘检测器的data input端,而SUT则接至clock input端。当EN为高电位时,SUT 正缘产生后会取样到Hi,因此讯号E马上pull Hi。若此时我们选择remove为/8时,如图十二Case3所示,EN讯号会维持4*TSUT的时间后转为低电位,因此当SUT下一个正缘产生后,其会取样到Low,促使讯号E pull down。
由图中可以看出,讯号SUT经转换后成功remove掉3.5(=4-0.5)个cycles,且SUT讯号只经过一颗ED。如此一来将可拉长stable region,维持放大倍率,并也不会因为让待测讯号路径太长而改变原先之抖动量。因此利用上述所提出抖动放大技术搭配脉波吞噬观念之单撷取量测法,将可在任何频段下线性放大待测时脉抖动,以利后段时间-数位转换电路之抖动量解析,并解决其因制程限制所造成准确度不足的问题。
时间-数位转换电路(Time-to-Digital Converter;TDC)
《图十四 所提出之时间-数位转换电路》
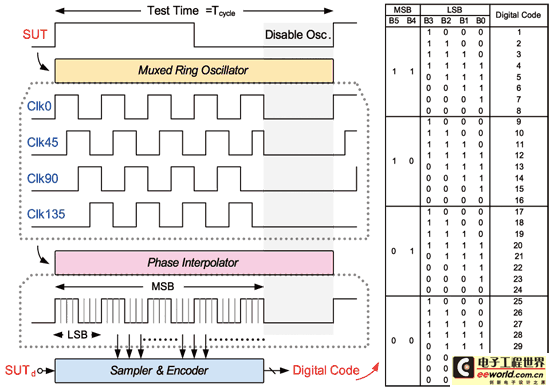
在本文中我们提出新的时间-数位转换电路,这是因为传统时间-数位转换电路基本上皆是使用多级缓冲器或是延迟单元来产生多相位讯号,然后藉由取样来得到数位码。然而以目前0.13-um的制程来说,其所能产生的最小缓冲延迟约为25-ps左右;亦即以整个系统来看,其能测试的最高解析度也等于25-ps,此规格在现今高速应用中已无法满足测试需求。
有鉴于此,我们将利用多工式振荡器搭配相位内插法,来实现一较高解析度之时间-数位转换电路。如图十四所示。其主要包含了一组多工式振荡器(Muxed oscillator)、相位内插电路(Phase Interpolator;PI)以及取样编码电路,当中多工式振荡器是用来产生多相位之参考讯号。相较传统使用open loop delay chain,close loop因有回授机制,所以会具有较准确的单位延迟时间,且较不易受到制程漂移之影响。另外因为是使用振荡原理来产生相位,所以可藉由测试振荡频推算出单位延迟时间,接着若再搭配使用内插电路技术,将可大幅提升测试解析度。
《图十五 多工式振荡器之电路架构图》
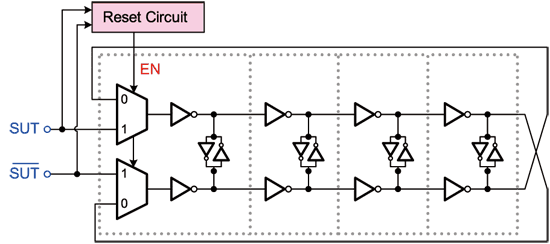
多工式振荡器是时间-数位转换电路中最为重要的电路,因为其必需依待测讯号的上升缘,来振荡出用来被取样之多相位高速讯号。如图十五所示,由两个多工器、四级延迟单元以及重置电路所组成。其称为多工式振荡器是因为此电路具有两种操作模式,分别为振荡模式(oscillating mode)与闩锁模式(latching mode),模式之切换则由重置电路来决定。
相关操作原理如下。当待测讯号正缘产生时,重置电路会输出EN为低电路,此时多工器选择到0。以图十五所示,此时回路可视为一差动振荡器,持续稳定提供多相位之高速参考讯号。然而通常于各系统中抖动量皆不会超越半个周期,也就是(1/2)xUI,所以其实每个周期内的抖动测试皆会于半个周期内结束,因此只需于待测电路的半个周期里产生出待取样讯号。换句话说就是只需让多工式振荡器工作半个周期后即可关闭。
因此当待测讯号负边缘一产生,重置电路会强制EN为高电位,此时多工器将由1的路径输出,也就是切换至闩锁模式。由图中可看出,此时整体振荡回路已被切断,输入即为待测讯号,各延迟单元的输出不是待测讯号的延迟、就是待测讯号的反向延迟,直至正边缘又产生后,才会恢复振荡模式以利抖动之测试。
传统时间-数位转换电路设计上,通常会受到制程所能产生的最小闸延迟所限定。为了克服此问题,我们采用了常见的相位内插电路,来产生小于一个延迟单元可提供的延迟时间。相位内插电路的直觉想法是希望能够在两个相邻相位的信号之间产生一个新的信号,而其相位会介于这两相邻相位信号间,进而达到提供更高相位解析度的信号 [10]。
小结
以上我们介绍内建抖动测试想法与架构,主要是想藉由放大输入抖动量来解决传统测试法无法测试低抖动量的问题,并搭配上多工式振荡之时间-数位转换电路,来提升整体系统解析度。此外也依电路操作特性提出一脉波吞噬电路,使得此测试系统将可于各频段进行自我测试,将不会因操作速度而影响测试品质。接着下一章节中,我们将利用HSpice来验证所提出之方法与架构。
《图九 抖动放大电路之架构图与时序图》

周期对周期抖动量即为后一个周期边缘En+1和前一个周期边缘En之相位误差,因此若要实现抖动量放大就必需将En和En+1间之边缘时间差拉大。在本文中将采用电流对负载充放电之原理来达到抖动放大之功能。我们以图九来说明其操作原理。
抖动放大电路基本上是由两组不同电流量之电荷帮浦(Charge Pump;CP)与决策电路(Decision Circuit;DC)所组成,而分别由待测讯号SUT、一个周期延迟后之讯号SUTd与两者之组合来控制。其最基本的想法为利用不同充电斜率(即充电速度)搭配讯号不同起始点(即转态边缘)之特性,来合成出具有较大抖动量的时脉边缘。而为了清楚解释其放大原理,我们将SUT(S)与SUTd((Sd)依相位关系区分成四个区间,然后分别探讨在不同区间内的操作情形。如表一所示。
(表一) 电荷帮浦操作状态表


搭配图九与表一之叙述,从中可以得知在初始状态时因SUT与SUTd为低电位,开关皆turn off,所以并无任何电流对负载做充电因此输出结果(f1、f2)将为低电位(VL)。但若当两个phase间有抖动存在时,SUT会为高电位而SUTd为低电位。此时f1会以(n+1)倍的电流对负载充电pull up,而f2因S3 turn off所以将保持前一状态的低电位。接着经过Δτ的时间后,SUTd也pull high,促使S3 turn on、S1 turn off,此时f1和f2将一起以I的速度往高电位移动。但是仔细观察Region II和Region III之过程,因在Δτ的这段时间里f1先以较快的速度启动,若Region III在相同充电的斜率条件下(电流量皆为I)其会先到达稳态位准;而接着再经过n*Δτ时间后,f2才也会到达此位准。此时从图九中可以看出f1、f2与所设定的临界电压(Vth)有两个交点,若用两组决策电路将转态点判断出来即可产生两组不同相位差的输出讯号(Out1、Out2)。所以利用上述之条件,我们可以简单以公式一来表示出输出与输入间的关系:
《公式一》
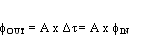
其中fOUT为Out1、Out2间的相位差(放大后之周期对周期抖动量)、fIN为SUT、SUTd间的相位差(放大前之周期对周期抖动量),而A即代表放大倍率。
利用上述概念,本创作即可将时脉讯号之周期对周期抖动量加以放大,来弥补时间-数位转换电路的不足。然而单纯光靠电流充电能力的行为模式来达成放大目的,会面临电路操作瓶颈进而导致测试误差产生,例如放大倍率的非线性或是操作频率变化等,接下来我们会针对这些效应提出解决之道。
抖动放大电路及Pulse Remover设计的分析
(表二) 符号表示

在抖动放大电路基本设计中,因为是使用电流对负载充放电之速率来达到抖动放大,因此先针对充放电位准以及时间作定义。如表二所示。
图十(a)中,通常抖动放大电路在低速率操作时,因其抖动量相较于半个周期时间所占的比例较小,因此电荷帮浦输出(f1、f2)到达高稳态点时间(ts1、ts2)通常会小于负缘转态点时间tf。
《图十 抖动放大电路时序图:(a)Case 1 : tf>ts2;(b)Case 2 : tf≈ts2;(c)Case 3 : tf

所以在此频段操作因有足够的稳态区间(stable region),其经决策电路后产生之输出相位差fOUT相较于输入相位差fIN几乎能维持定值,也就代表放大倍率A为constant。但若当待测时脉频率上升后,如图十(b)所示,随着讯号周期缩短tf之发生点提前,在tf非常接近但大于ts2时,抖动放大电路依然可勉强维持住放大倍率,所以此时即称为操作临界值。但假若不幸在所使用的应用中tf发生较大的变异或是操作频率继续往上升,导致ts2比tf晚发生,则放大倍率将开始产生非线性的变化。
从图十(c)可观察出在正常的操作模式下f1与f2最后皆会回到稳态位准VH、VL。但假若转态边缘tf在尚未稳定前就出现,则f1与f2之电压会被强制维持在新的位准上,也就是VH’(=VH-ΔV)与VL’(= VL +ΔV)。这个现象虽对于第一个周期(initial stage)之放大倍率没有造成影响,但是从图中得知,在下一个周期(next stage)中因为f1、f2电压起始位准点有了变化,所以经充电后与临界电压Vth的交点必然随之改变。换句话说就是voltage domain variation将转换成time domain之phase error,此时即会造成放大倍率变动。因此周期对周期抖动放大电路需操作在wide range之应用时,就必需利用一些机制控制稳态时间点ts比负缘转态点 tf早发生,如此才不会造成放大倍率的失真。有鉴于此,本文将提出一个使用脉波吞噬观念之单撷取量测方式来改善之。
脉波吞噬之单撷取量测方式
《图十一 脉波吞噬概念图》

以上述讨论可知,若要实现tsf,不外乎是将稳态时间点往前拉会或者是延迟负缘转态点产生之时间。以电路实现角度而言,因ts是电流对负载充电后所产生的电压与高电位VH之交集,所以电流越大、回到稳态点能力越强,相对其出现时间会越早。但抖动放大的产生就是藉由不同速率电流之差所得,想必然放大倍率也将受到影响。所以为了兼顾放大倍率与电流量间trade-off,本文将采用延迟tf之作法来维持不同操作频率下的抖动放大倍率。
如图十一case1所示为一低频操作时的示意图。为了让抖动放大电路的放大倍率维持定值,待测讯号的ts必需小于tf,而worst case会发生在ts等于tf的时间点,此时稳态区间几乎会近似于零,也就是说放大倍率会非常不稳定。
为了改善这个问题,以先前的说法就必需将tf时间点做延迟。简单来看就是把测试速度放慢,利用脉波吞噬电路移除掉0.5个周期,来换取稳态区间之宽度。如图所示,若把case1的讯号做处理后成为TAIn1,其负缘转态时间点发生的时间往后延迟了Δτ(=tfn-tf=Tcycle/2),这代表着稳态区间随之放大2倍。因此若把待测讯号的频率增加后,其因具有足够的稳态时间,所以放大倍率将不受到clock variation和频率变动之影响。
但在图十一 Case2中,待测时脉讯号操作速度持续上升(约为Case1的两倍),可以很明显观察到若不采用脉波吞噬机制,ts已远远超越了tf,此时抖动放大电路之放大倍率已为非线性操作;但若加入脉波吞噬的机制后,因待测讯号速度太快,在相同充放电的速率条件下,ts也非常靠近tfn,放大倍率变异的问题还是存在。所以由此可知真正要达到wide range的操作,不管在任何频率下,皆需要拥有相同的稳态区间,才会真正得到constant之放大倍率。有鉴于此,我们将脉波吞噬的机制稍做修改,将不再维持固定移除0.5个周期,而是随着待测物的频率每增加一倍而随之变化,其remove number可由公式二表示之:
《公式二》
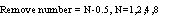
其中N为频率变化率。在本文中所提出的例子因为要达到数十MHz~1.6GHz之操作,所以将100MHz定为基准,频率每增加一倍就必需改变remove number来维持放大倍率。如图十二所示。
《图十二 于各操作频段间之脉波吞噬概念图》

以电路的角度而言,要实现图十二脉波吞噬电路其实不难,只要将待测讯号依频段经过相对应的除频器即可实现。但实际上若直接把待测讯号经过除频器来达到脉波吞噬,依参考文献[9]之说法,该讯号的抖动也同时间会被放大,约为 √n倍。此外,除16的电路最少需要4组DFF来实现,代表待测讯号到达抖动放大电路前就必需经过许多transistor,进而受到power noise或是thermal noise干扰导致抖动上升,这将会严重影响量测准确度。
以边缘检测达到脉波吞噬效果
《图十三 (a)所提出之抖动放大电路;(b)边缘检测电路操作示意图》

因此本文将采用边缘检测(edge detection)之技术来达到脉波吞噬的效果,如图十三(a)所示。其主要包含两大方块:边缘检测器与脉波吞噬电路。首先,当待测讯号启动后,为了维持放大倍率,需先进行pulse remove的动作。以图十三(b)为例,SUT为待测讯号,EN为脉波吞噬电路所产生,E为经过处理后的待测讯号。其中脉波吞噬电路是由MUX所实现,其可藉由控制s脚位来选择EN讯号为SUT之/2、/4、/8、/16的结果。
此外EN接至边缘检测器的data input端,而SUT则接至clock input端。当EN为高电位时,SUT 正缘产生后会取样到Hi,因此讯号E马上pull Hi。若此时我们选择remove为/8时,如图十二Case3所示,EN讯号会维持4*TSUT的时间后转为低电位,因此当SUT下一个正缘产生后,其会取样到Low,促使讯号E pull down。
由图中可以看出,讯号SUT经转换后成功remove掉3.5(=4-0.5)个cycles,且SUT讯号只经过一颗ED。如此一来将可拉长stable region,维持放大倍率,并也不会因为让待测讯号路径太长而改变原先之抖动量。因此利用上述所提出抖动放大技术搭配脉波吞噬观念之单撷取量测法,将可在任何频段下线性放大待测时脉抖动,以利后段时间-数位转换电路之抖动量解析,并解决其因制程限制所造成准确度不足的问题。
时间-数位转换电路(Time-to-Digital Converter;TDC)
《图十四 所提出之时间-数位转换电路》

在本文中我们提出新的时间-数位转换电路,这是因为传统时间-数位转换电路基本上皆是使用多级缓冲器或是延迟单元来产生多相位讯号,然后藉由取样来得到数位码。然而以目前0.13-um的制程来说,其所能产生的最小缓冲延迟约为25-ps左右;亦即以整个系统来看,其能测试的最高解析度也等于25-ps,此规格在现今高速应用中已无法满足测试需求。
有鉴于此,我们将利用多工式振荡器搭配相位内插法,来实现一较高解析度之时间-数位转换电路。如图十四所示。其主要包含了一组多工式振荡器(Muxed oscillator)、相位内插电路(Phase Interpolator;PI)以及取样编码电路,当中多工式振荡器是用来产生多相位之参考讯号。相较传统使用open loop delay chain,close loop因有回授机制,所以会具有较准确的单位延迟时间,且较不易受到制程漂移之影响。另外因为是使用振荡原理来产生相位,所以可藉由测试振荡频推算出单位延迟时间,接着若再搭配使用内插电路技术,将可大幅提升测试解析度。
《图十五 多工式振荡器之电路架构图》

多工式振荡器是时间-数位转换电路中最为重要的电路,因为其必需依待测讯号的上升缘,来振荡出用来被取样之多相位高速讯号。如图十五所示,由两个多工器、四级延迟单元以及重置电路所组成。其称为多工式振荡器是因为此电路具有两种操作模式,分别为振荡模式(oscillating mode)与闩锁模式(latching mode),模式之切换则由重置电路来决定。
相关操作原理如下。当待测讯号正缘产生时,重置电路会输出EN为低电路,此时多工器选择到0。以图十五所示,此时回路可视为一差动振荡器,持续稳定提供多相位之高速参考讯号。然而通常于各系统中抖动量皆不会超越半个周期,也就是(1/2)xUI,所以其实每个周期内的抖动测试皆会于半个周期内结束,因此只需于待测电路的半个周期里产生出待取样讯号。换句话说就是只需让多工式振荡器工作半个周期后即可关闭。
因此当待测讯号负边缘一产生,重置电路会强制EN为高电位,此时多工器将由1的路径输出,也就是切换至闩锁模式。由图中可看出,此时整体振荡回路已被切断,输入即为待测讯号,各延迟单元的输出不是待测讯号的延迟、就是待测讯号的反向延迟,直至正边缘又产生后,才会恢复振荡模式以利抖动之测试。
传统时间-数位转换电路设计上,通常会受到制程所能产生的最小闸延迟所限定。为了克服此问题,我们采用了常见的相位内插电路,来产生小于一个延迟单元可提供的延迟时间。相位内插电路的直觉想法是希望能够在两个相邻相位的信号之间产生一个新的信号,而其相位会介于这两相邻相位信号间,进而达到提供更高相位解析度的信号 [10]。
小结
以上我们介绍内建抖动测试想法与架构,主要是想藉由放大输入抖动量来解决传统测试法无法测试低抖动量的问题,并搭配上多工式振荡之时间-数位转换电路,来提升整体系统解析度。此外也依电路操作特性提出一脉波吞噬电路,使得此测试系统将可于各频段进行自我测试,将不会因操作速度而影响测试品质。接着下一章节中,我们将利用HSpice来验证所提出之方法与架构。
内建式抖动测量技 相关文章:
- 内建式抖动测量技术(上)(01-09)
- 内建式抖动测量技术(下)(01-09)
- 频宽、取样速率及奈奎斯特定理(09-14)
- 为什么要进行信号调理?(09-30)
- IEEE802.16-2004 WiMAX物理层操作和测量(09-16)
- 为任意波形发生器增加价值(10-27)
