运算放大器电路中固有噪声的分析与测量(第一部分):引言与统计数据评论
学方法估算标准偏差。举例来说,如果我们从模数 (A/D) 转换器中获得大量采样,那么我们就能运用方程式 1.4, 1.5 及 1.6 来计算噪声信号的平均偏差、标准偏差以及 RMS 值。附录中的示例 1.3 显示了在 Basic程序中如何运用上述方程式。我们在附录中还列出了一组更全面的统计方程供您参考。 方程式 1.4、1.5、1.6:离散数据的统计方程 本文最后要介绍的概念是噪声信号的叠加。为了叠加两个噪声信号,我们必须先了解信号是否相关。来自两个不同信号源的噪声信号彼此不相关。举例来说,来自两个不同电阻器或两个不同运算放大器的噪声是彼此不相关的。不过,噪声源通过反馈机制会产生关联。什么是相关噪声源叠加呢?一个很好的实例就是带噪声消除功能的耳机,其可通过累加反向相关的噪声来消除噪声。方程式 1.7 显示了如何叠加相关噪声信号。请注意,就带噪声消除功能的耳机而言,相关系数 C 应等于 - 1。 在大多数情况下,我们都要叠加不相关的噪声源(见方程式 1.8)。在这种情况下叠加噪声,我们要通过勾股定理得到两个矢量噪声的和。图 1.5 显示了叠加噪声源的情况。我们通常可做近似地估计,如果一个噪声源强度为另一个的三分之一,较小的噪声源可忽略不计。 图 1.5: 噪声勾股定理。 本文总结与后续文章介绍: 在关于噪声的系列文章中,本文介绍了噪声的概念,谈论了噪声分析所需的一些统计学基本原理。本系列文章中都将用到这些基础知识。本系列文章的第二部分将介绍运算放大器的噪声模型,并给出计算总输出噪声的一些方法。致谢: 特别感谢以下人员提供的技术信息: 德州仪器 (TI) Burr-Brown产品部 参考书目: Robert V. Hogg与Elliot A Tanis共同编著的《概率与统计推断》,第三版,麦克米兰出版公司 (Macmillan Publishing Co)出版; C. D. Motchenbacher与 J. A. Connelly共同编著的《低噪声电子系统设计》,A Wiley-Interscience Publication出版。 关于作者: Arthur Kay 现任 TI 的高级应用工程师。他专门负责传感器信号调节器件的支持工作。他于 1993 年毕业于佐治亚理工学院 (Georgia Institute of Technology) 并获得电子工程硕士学位。他曾在 Burr-Brown 与 Northrop Grumman 公司担任过半导体测试工程师。 附录 1.1: 附录 1.2: 附录 1.3: 附录 1.4: 附录1.5: 作者:德州仪器公司高级应用工程师,Art Kay 

方程式 1.7: 叠加随机相关信号 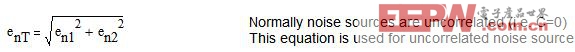
方程式1.8: 叠加随机不相关的信号 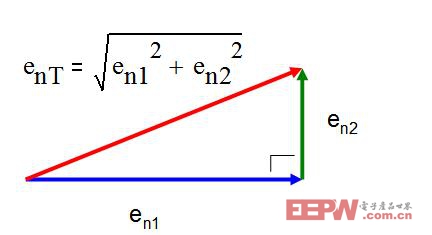
Rod Burt,高级模拟 IC 设计经理
Bruce Trump,线性产品经理
Tim Green,应用工程设计经理
Neil Albaugh,高级应用工程师
例 1: 本例中,RMS 值与标准偏差不等。通常说来,如果存在 DC 元件的话,标准偏差与 RMS 值不等(即非零平均值)。 
例2:本例中,RMS 等于标准偏差。通常说来,如果不存在 DC 元件的话,标准偏差与 RMS 相等(即零平均值)。 
例 3:计算平均偏差、标准偏差及 RMS 值所采用的 Basic 程序 
采用概率分布函数的统计方程 
采用适用于测量数据的统计方程 
运算放大器 固有噪声 宽带噪声 热噪声 闪烁噪声 相关文章:
- 用于电压或电流调节的新调节器架构(07-19)
- 大功率LED照明恒流驱动电源的设计(10-15)
- AD7656的原理及在继电保护产品中的应用(06-18)
- 如何看懂电源电路图(06-28)
- 电源高位跟踪系统的设计与实现(07-17)
- 基于DSP的单相精密电源硬件设计(07-24)
