基于同伦算法的逆变电源特定消谐法的研究

0 引 言
随着逆变器的大量应用，逆变器产生的谐波会给电网、电器设备、通信网络等带来严重危害，这使得消谐逆变器的研究越来越重要。同时为满足高压大功率应用领域的需要，采用主电路为级联多电平逆变器，实现波形的多重移相叠加。特定谐波消除(SHEPWM)方法。能使逆变器开关频率降低，消除特定低次谐波，减少电流脉动，输出波质量高等优点，因此对SHE技术的研究具有明显的理论意义和广阔的工程开发前景。
由于消谐PWM逆变器的数学模型为非线性超越方程组，该方程中有三角函数，并且是超越方程，存在多组解。通常采用牛顿法求解该模型，但由于牛顿法的局部收敛性质，需要找到与准确值较为接近的初值，否则迭代不收敛，这比较困难，且不利于在线计算，而同伦算法求解该模型可有效地克服上述缺点

l 级联多电平逆变器结构与控制设计
1．1 级联多电平逆变器结构
图1显示主电路为级联多电平逆变器的单相拓扑结构，每个逆变器模块结构相同，通过一个单相全桥逆变器表示。级联多电平逆变器的结构允许每个模块的分离控制，模块的数量与要求的电压源的数量是相等的。电平数NL和模块数M的关系公式为：

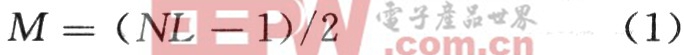
模块数即单相H桥逆变器的个数，它们串联连接产生一个多电平的输出电压；总输出电压与每个模块的输出电压之和相等。即为：

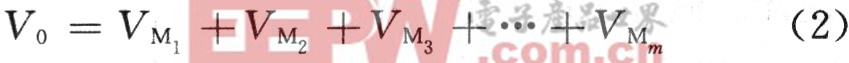
式中：VMm为第m个模块的输出电压。
每个模块有它自己的直流电压(VDC)和4个开关装置，如第m个模块的开关装置是S1m，S2m，S3m和S4m，(表1中开为“1”，关为“0”)。如图2所示每个模块能产生一个三电平输出：+VDC，0，-VDC。通过这4个开关装置能有顺序地将直流电压到交流边。如表1所示输出电压与一个五电平模块结构多电平逆变器的功率装置的开关状态相对应。因为1个输出电压包括5个电平+2VDC，+VDC，0，-VDC，-2VDC，需要的模块数是2。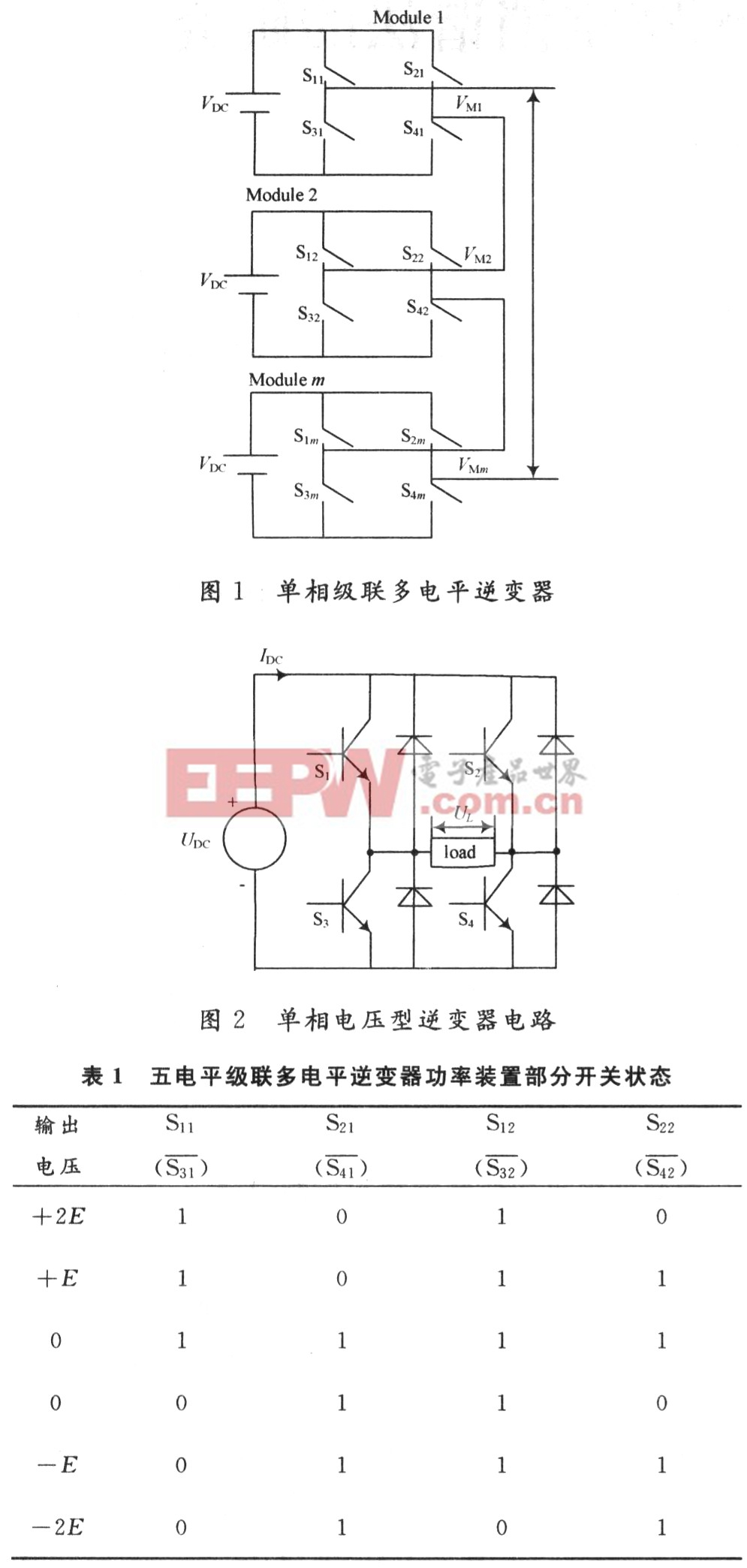

1．2 控制设计
表2所示是一个五电平的级联多电平逆变器控制设计。假设级联多电平逆变器的每个模块的直流电压VDC=20 V，如表2中的描述知级联多电平逆变器的操作大部分取决于模块1，只有当q>0.5时，模块2才参与运行。尽管在五电平级联多电平逆变器中需要8个功率装置，这8个装置并不全被利用，此种情况减少了功率装置的电压应力。对于如图2所示的单相逆变器，基波幅值q最大值为1.0，再大将导致一些迭代法(如牛顿迭代法)无法收敛。

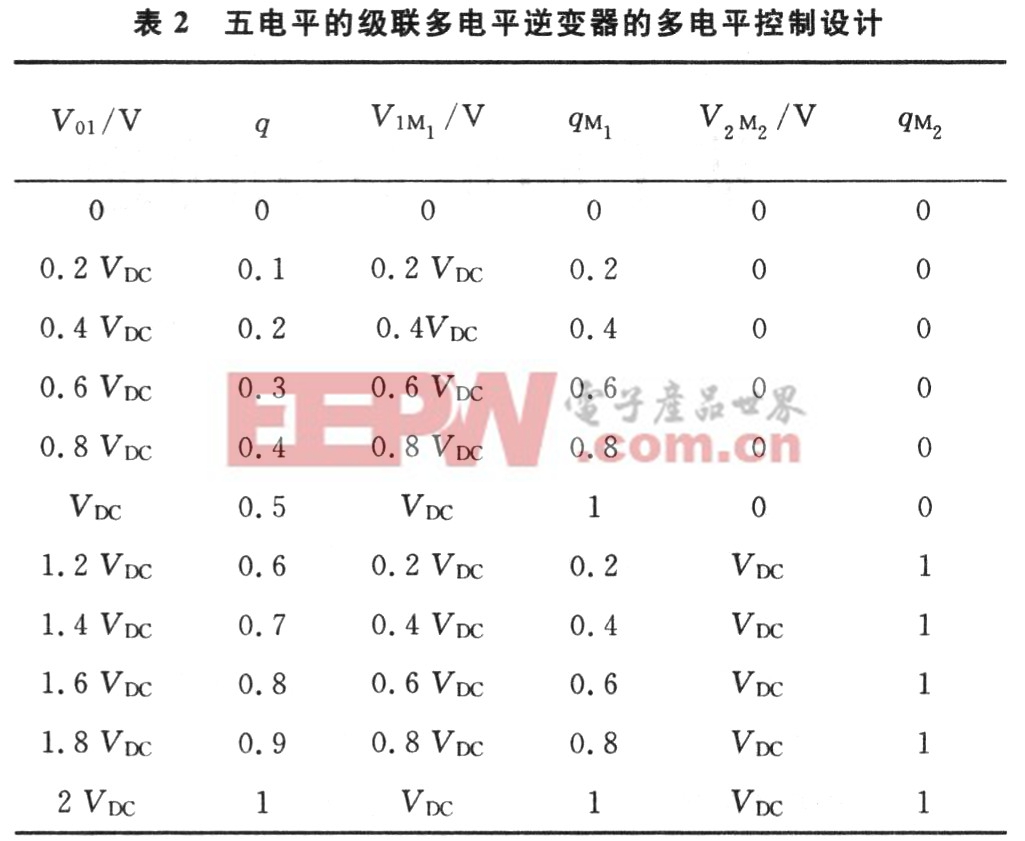
在表2中：VDC为直流侧线电压；V01：逆变器的输出基波电压；q：基波幅值；V1M1(V2M2)：模块1(模块2)输出的基波电压；qM(qM)：模块1(模块2)的基波幅值。

2 消谐PWM模型的建立
消谐PWM控制的基本方法是：通过PWM控制的傅里叶级数分析，得出傅里叶级数展开式，以脉冲相位角为未知数，令某些特定的谐波为零，便得到一个非线性方程组，该方程组即为消谐PWM模型，按模型求解的结果进行控制，则输出不含这些特定的低次谐波。消谐模型的建立与PWM控制方式是相关的，以电压型逆变器为例，根据不同的PWM特点，建立的模型可归纳为两种：即单极性脉冲控制模型和双极性脉冲控制模型。这里只讨论单极性脉冲控制模型，如图2所示，在这种控制方式下，为了降低开关损耗，可使同一桥臂中的一个开关管(如S2或S4)在半个周期内一直处于导通状态。PWM波形由桥臂的另一个开关管的通断实现。图3为单极性脉冲控制输出电压波形，单极性波形的傅里叶级数表达式为：

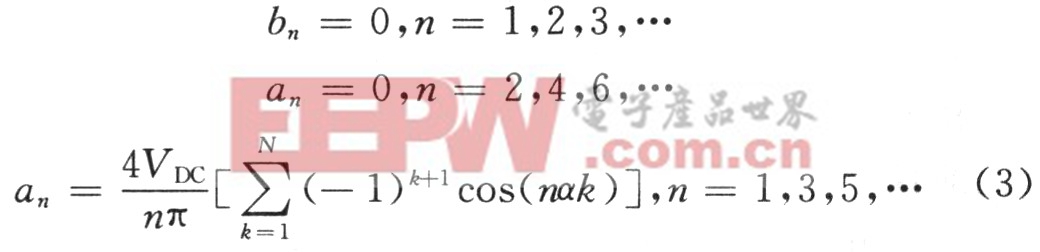
单极性脉冲波形与双极性脉冲地消谐模型相类似，为了方便说明，以下的论述均以单极性脉冲为例，但其原理完全适用于双极性脉冲。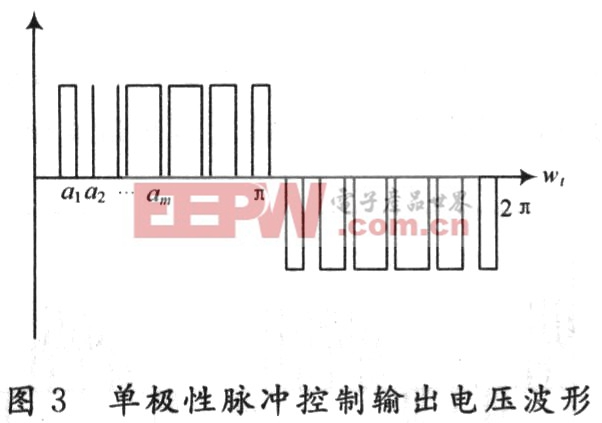

取直流侧线电压为VDc=1，取开关角为8，如果选择性的消除N一1个低阶奇次谐波(如3，5，7，9…)在此选择消除7个低次的谐波3，5，7，9，11，13，15，得到下面非线性方程组(4)，给出使基波幅值q为某一给定值，其余k次谐波的幅值为0，即达到消谐的目的，只需解下列方程组：

解非线性方程组(4)，便得PWM波的各开关角，然后根据对称特性可以得到整个周期的各个开关角。求解该方程组，可得到一组[0，π／2]内的开关角，当然，这些开关角应满足以下条件：

0α1α2α3α4α5α6α7α8π／2
式(4)为非线性方程组，一般采用牛顿迭代法求解，但是该求解过程是否收敛与所取的初值有很大的关系。使用时由于求解非线性方程组存在较大困难以及存储脉冲相位角需要很大的存贮空间，因而在相当程度上制约了它的应用。目前该方法的应用仅限于离线控制。

3 同伦算法的建立
3．1 同伦算法
同伦方程的数值解法有2种：同伦延拓法；参数微分法。采用参数微分法将非线性方程组(4)简写为：
F(a)=0 (5)
式中，F：D∈Rn→Rn。令a*是方程组(5)的解。
非线性超越方程组(5)，一般采用牛顿迭代法求解，但该方法对初值的选取要求较为严格，即要求初始近似解a0与解a*充分靠近，才能使迭代数{ak}收敛于a*。实际计算中要找到满足要求的迭代初始值往往很困难，如果给出的初始值导致迭代不收敛，就需要重新给初始值再计算，这样就大大降低了求解速度，难以实现实时控制。为了解决这个问题，这里尝试用同伦法求解。同伦法是一种用于非线性方程组数值求解的新方法，具有全局收敛和收敛速度快等优点，其基本的思想是：对于该方程组，引人参数t，构造一族映射H，使当t为某一特定值(例如t=1)时，H就是映象F，而当t=0时，得出方程组F0(a)=0的解a0是已知的。也就是说，构造一簇映射H：D×[O，1]∈Rn+1→Rn，代替单个映射F，使H满足条件：