电流型控制原理及特点分析

一、电流型控制原理及特点

原理：

电流型脉宽调制(PWM)控制器是在普通电压反馈PWM 控制环内部增加了电流反馈的控制环节,因而除了包含电压型PWM 控制器的功能外,还能检测开关电流或电感电流,实现电压电流的双环控制。控制原理框图如下图(图1)所示。

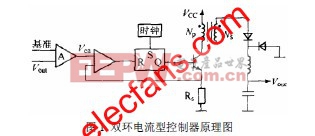
图 1 双环电流型控制器原理图

从图 1 可以看出,电流型控制器有两个控制闭合环路:一个是输出电压反馈误差放大器A,用于与基准电压比较后产生误差电压;另一个是变压器初级(电感)中电流在Rs 上产生的电压与误差电压进行比较,产生调制脉冲的脉宽,使得误差信号对峰值电感电流起着实际控制作用。系统工作过程如下:假定输入电压下降,整流后的直流电压下降,经电感延迟使输出电压下降,经误差放大器延迟Vca 上升,占空比变化,从而维持输出电压不变,在电流环中电感的峰值电流也随输入电压下降,电感电流的斜率di/dt 下降,导致斜坡电压推迟到达Vca,使PWM 占空比加大,起到调整输出电压的作用。由于既对电压又对电流起控制作用,所以控制效果较好在实际中得到广泛应用。

特点：

a)由于输入电压Vi 的变化立即反映为电感电流的变化,不经过误差放大器就能在比较器中改变输出脉冲宽度(电流控制环),因而使得系统的电压调整率非常好,可达到0.01%V, 能够与线性移压器相比。

b)由于双环控制系统内在的快速响应和高稳定性,反馈回路的增益较高,不会造成稳定性与增益的矛盾,使输出电压有很高的精度。

c)由于Rs 上感应出峰值电感电流,只要Rs 上电平达到1V,PWM 控制器就立即关闭,形成逐个脉冲限流电路,使得在任何输入电压和负载瞬态变化时,功率开关管的峰值电流被控制在一定范围内,在过载和短路时对主开关管起到有效保护。

d)误差放大器用于控制,由于负载变化造成的输出电压变化,使得当负载减小时电压升高的幅度大大减小,明显改善了负载调整率。

e)由于系统的内环是一个良好的受控电流放大器,所以把电流取样信号转变成的电压信号和一个公共电压误差放大器的输出信号相比较,就可以实现并联均流,因而系统并联较易实现。

二、峰值电流控制与平均电流控制的比较

峰值电流模式控制和平均电流模式控制相比主要具有以下缺点:

(1)对噪声敏感，峰值电流模式控制是将电感电流的上升沿(即开关电流)同设定的电流值相比较,当瞬态电流达到设定值,PWM比较器输出翻转将功率开关管关断。电感电流上升到设定值的坡度即(Vin-Vout)/L 很小,特别是Vin 小时坡度更小,所以这种控制方法易受噪声干扰。每次开关管通断时都会产生噪声尖峰,并且耦合到控制电路的一个小电压就能使开关管迅速关断,使电路处于次谐波运作模式产生很大的纹波,所以对于峰值电流控制模式,电路布局和噪声旁路设计对电路的正常工作很重要,平均电流模式控制可以简化这部分工作。

(2)需斜坡补偿,对于峰值电流控制,当占空比大于50%时扰动电流引起的电流误差越变越大。所以尖峰电流模式控制在占空比大于50%时,电路工作不稳定,需给PWM比较器加坡度补偿以使电路稳定。内部电流环的增益尖峰会使相移超出范围,导致电路工作不稳定,使电压环进入次谐波振荡。这时在连续固定的驱动脉冲时,输出占空比却在变化,这时也需斜坡补偿来抑制次谐波振荡。

(3)具有尖峰值/平均值误差,在尖峰电流控制模式中,随着占空比的不同,电感电流的平均值亦不同,通过斜坡补偿可以获得不同占空比下一致的电感电流,但这也增加了电路的复杂性。另外电感电流的平均和峰值间也存在差值,在BUCK 电路中由于电感电流的纹波相对电感电流的平均值很小,并且存在电压外环的校正作用,所以峰值和平均值的这种误差可以忽略;在BOOST 电路中,峰值要跟随输入电网的正弦波,所以和平均值间的误差很大,在小电流时,尤其是电流不连续时,如每半周期输入电流过零时,这种误差最大,它会使输入电流波形畸变。这时就需要一个大电感来使电感电流的纹波变小,但这将使电感电流的坡度变窄,减小抗干扰能力。

平均电流控制和峰值电流控制相比的优点是:

① 具有高增益的电流放大器,平均电流可以精确地跟踪电流设定值。这点应用在高功率因数控制电路中尤其重要,此时用一个小电感就能获得小于3%的谐波畸变,并且即使电路模型由连续电流模式过渡到不连续电流模式,平均电流法也能很好地工作;

② 噪声抑制能力强,因为当时钟脉冲使功率开关管开通后,晶振幅度迅速降到了一个低值;

③ 无须斜坡补偿,但为了电路工作稳定,在开关频率附近必须限定环路增益;

④ 平均电流法可应用在任意电路拓扑上,既能控制BUCK和Flyback 电路的输入电流,又能控

制Boost 和Flyback 电路的输出电流。若加入到PWM比较器输入端的波形坡