)”。
现以图1的统一模型为例,介绍这种分析方法。
设Ri为在状态I期间Vs对Ci充电的等效阻抗，r是电容器的等效串联阻抗（ESR），r′为开关管的导通电阻，则有
Ri=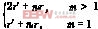
（1）
设Qi′和Qij′分别为Ci和Cij在状态II放掉的电量，也即负载在一个周期内通过的电量；设Qi和Qij分别为Ci和Cij在状态I的充电电量，由于构成Ci的各个电容Cij串联充电，并联放电，所以有
Qi=Qij
Qi′=niQij (2)
Cij在状态II失去的电量，应在状态I得到充分地补充，于是
Qij=Qij′
Qi′=niQi (3)
根据电容，电量和电压的关系（Q=CU），有
Vci(t1)－Vci(t0)=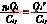
(4)
而
Qi′=ILTs=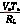
(5)
根据在状态I期间，电容电压按指数规律上升的原则，有
Vci(t1)－Vci(t0)=[Vs－(ni－1)Vd－Vci(t0)][1－exp(－DTni/RiCij)](6)
由以上各式可以推出
Vci(t1)=Vs－(ni－1)Vd－
(7)
假设Co很大，即Vo的纹波很小，在状态II结束时，则有
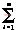Vci(t0)/ni－
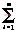(ni－1)Vd=Vo(8)
从而可以得到：
Vo=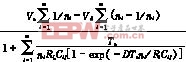
(9)
将式（9）的指数项展开成幂级数，并忽略二次以上各项，则有
Vo=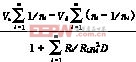
(10)
式（10）即为脉宽调制（PWM）下，典型开关电容DC/DC变换器的稳态电压的通用表达式。
4 开关电容DC/DC变换器的控制方法
式(9)中，我们称DTsni/RiCij为该串并电容组合结构的特征系数，用Ki表示,根据Ki的取值，一般可以分为以下三种工作情况。
1)脉宽调制模式(PWM)
当各个串并电容组合结构的特征系数Ki均较小时，式(9)中的指数函数的幂级数展开式的二次以上各项可以忽略不计，从而式（9）可简化为式(10)，式(10)表明采用PWM方式，可以获取调制效果，改变工作频率对于变换器的输出电压没有明显影响，我们称之为脉冲宽度调制模式。
2)频率调制模式(FM)
当各个串并电容组合结构的特征系数Ki均较大时,式(9)可简化为
Vo=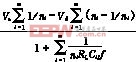
(11)
式(11)表明，采用PWM方式，已经无法获得明显的调制效果，而采用FM方式，可以起到调制输出电压的作用，我们称之为频率调制模式。
3)过渡模式(混合调制模式)
当存在至少一个串并电容组合结构的特征系数Ki不很大，也不很小时，式(9)中的指数项不能线性化，开关电容DC/DC变换器的输出电压受到工作频率和占空比的双重影响，称之为过渡模式。
一般情况下，三种工作模式的分界线可确定如下[2]：
Ki>3时，开关电容DC/DC变换器工作在FM模式；
0.2Ki3时，开关电容DC/DC变换器工作在过渡模式；
Ki0.2时，开关电容DC/DC变换器工作在PWM模式。
4)逐压控制模式
PWM动态响应速度较慢，只适用于DC/DC变换器，而逐压控制方法具有较好的动态响应，采用同样结构的开关电容变换器，可实现DC/AC变换和构成失真小的DC/AC变换器。
现以图3的基本开关电容DC/DC变换器为例阐述其工作原理，控制电路原理图如图4所示。
图4 基本开关电容DC/DC变换器逐压控制电路原理图
变换器启动后，当输出超过Vo＋Ve或振荡脉冲为负时，S12关断，S11导通；当输出低于Vo－Ve且振荡脉冲为正时，S12导通，S11关断。Vo是输出电压设计值，2Ve为允许纹波电压峰－峰值。通过振荡器提供的脉冲信号，可以保证在变换器启动初始即使Vo很低（或为零）C1也有被充电的机会，而当Vo建立起足够的电压后，通过逻辑电路封锁振荡器脉冲。这样，在启动初期，S11,S12受振荡器强制控制，以确保启动成功，稳定后振荡器不起作用，开关管完全由输出电压反馈控制。这就是逐压反馈控制的基本原理，通过这种控制方法可以使输出电压限制在所设计的动态范围之内。
5 开关电容DC/DC变换器的效率分析
5.1 基本效率分析
从能量的角度，效率η可以定义如下：
η=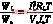
(12)
式中：WL和Ws分别是负载消耗和电源供给的能量；
IL和Is分别是负载电流和电源电流的平均值；
T为工作周期。
WL和Ws也可写作
WL=QLVL，Ws=QsVs
式中：QL和Qs分别是流过负载及电源流出的电量；
VL为负载电压。
于是，效率为
η=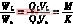
(13)
式中:M称为变换器的电压变比，M=VL/Vs；
K称为变换器的本征电压变比，K=Qs/QL。
在理想条件下，效率η可以为1，即M=K，但通常η1，即M对于图1的基本开关电容变换器，则有
QL=Qs，η=M，K=1
上式表明，无论采取什么调制方式，基本开关电容变换器的效率是其电压变比，当变比很小时，变换器的效率就很低。这并不比线性变换器好多少，但是电路却复杂得多，因而没有多大实际意义。
5.2 改善效率的方法
采用串并电容组合结构可以提高开关电容DC/DC变换器的效率。以图2的二阶串并电容组合DC/DC变换器为例进行分析。
设状态I时的充电电量为Q，状态II时的放电电量为Q′，则利用等效电量关系法可得
Qs=Q=Q11
|
