一种改进的电压跟随PFCCukAC/DC变换器
交流电压频率,可以假设在一个开关周期TS内,输入电压保持不变。 定义输入电压为: vin(t)=|Vpsinωt|(7) 式中:Vp为输入电压的峰值; ω为输入电压的角频率。 由于在提出的变换器中,要求电感L1工作在DCM,而电感L2工作在CCM,故需知道它们工作在临界状态时的值,现推导如下: 在模式1,流过电感L1的电流iL1可表示为: iL1(t,t′)=Vpt′|sinωt|/L1(0t′iL1p(t′,t)=VpDTS|sinωt|/L1(8) 式中:TS为开关周期; D为开关S的占空比; t′为时间坐标,其原点为每一个开关周期中开关导通的时刻。 由伏秒平衡原理可得: VinDTS=(2VC-Vin)(1-D-Δ)TS(9) 由于要求电感L1工作在DCM,只需要保证输入电压vin(t)达到最大值时L1工作在DCM的边界,此时由伏秒平衡原理可得: VpDTS=(2VC-Vp)(1-D)TS (VC-VO)DTS=VO(1-D)TS(10) 把式(7)、式(10)代入式(9)可得: 在一个开关周期内电感电流iL1的平均值可表示为: 〈iL1(t)〉=iL1P(t,t′)(1-Δ)/2 =VpDTS(1-Δ)|sinωt|/2L1(12) 把式(9)代入式(10)可得: 上式就是改进的VFPFCCukAC/DC变换器电路的输入电流表达式,在半个输入电压周期电源的输入功率为: 式中: Pout=VO2/RL=D2VP2/4RL(1-D)2(15) 假设变换器的效率为η,根据功率平衡原理可得: ηPin=Pout(16) 即 由上面的分析可得,输入电感L1工作的临界值为: 下面推导电感L2工作的临界值,由于输出功率 Pout=〈iL2〉VO(19) 电感L2工作在CCM与DCM的临界条件时,在一个开关周期TS内,流过电感L2的平均值〈iL2〉为: 〈iL2〉=iL2P/2=(VC-VO)DTS/2L2(20) 图6电路的仿真波形 (a)输入电流iL的波形(b)电流iL1的波形 (c)电流iL2的波形 由式(19)、式(20)可得: Pout=(VC-VO)DTSVO/2L2 =VP2D2TS/8L2(1-D)(21) 只要电感L1的值小于其临界值,而电感L2的值大于其临界值,则可以保证输入电感L1工作于DCM,从而实现了VFPFC的功能,而输出电感L2工作于CCM,从而减小了器件的应力和输出电流纹波。 5仿真结果 设计要求如下:输入电压vin(t)=110sinωt,电源频率f=50Hz,输出电压VO=127V,输出功率PO=200W(RL=80Ω),开关频率fs=100kHz。仿真所选的参数为:输入电压vin(t)=110sinωt,其频率f=50Hz,输入电感L1=100μH,输出电感L2=1000μH,开关频率fs=100kHz,开关的占空比D=0.45。仿真的波形如图6所示。图6(a)为输入电流iL(t)的波形,由图可见,输入电流的包络线近似为正弦波,仿真得到的输入电流功率因数为0.995。图6(b)为电感L1上的电流iL1的波形,电感L1工作在DCM。电感L2工作于CCM,流过L2的电流波形如图6(c)所示。 6结语 在传统的CukDC/DC变换器中引入一个二极管,改变了其输入与输出电感之间的依赖关系。通过对输入电感工作于DCM的Cuk变换器的功率因数校正能力的分析,用一开关电容网代替原单个储能电容,从而提高了其功率因数校正能力。通过对所提的VFPFCCukAC/DC变换器的分析,找出了输入与输出电感工作的临界值。在所提出的变换器中,输入电感L1工作于DCM,以实现功率因数校正,输出电感L2工作于CCM,从而减小了器件应力和输出电流、电压纹波。MATLAB仿真与实验结果证实了理论分析的正确性。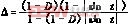 (11)
(11) 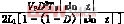 〈iL1(t)〉=(13)
〈iL1(t)〉=(13) 
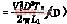 (14)
(14) ![]()
 平均输出功率为:
平均输出功率为: 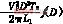
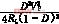 =(17)
=(17)  L1=(18)
L1=(18) 

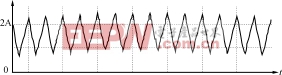
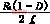 由式(15)、式(21)可得电感L2工作的临界值为:L2=(22)
由式(15)、式(21)可得电感L2工作的临界值为:L2=(22)
- 电源设计小贴士 1:为您的电源选择正确的工作频率(12-25)
- 用于电压或电流调节的新调节器架构(07-19)
- 超低静态电流电源管理IC延长便携应用工作时间(04-14)
- 电源设计小贴士 2:驾驭噪声电源(01-01)
- 负载点降压稳压器及其稳定性检查方法(07-19)
- 电源设计小贴士 3:阻尼输入滤波器(第一部分)(01-16)
