完美无谐波高压IGBT变频器

1前言

国外某公司利用一种新的高压变频技术，生产出功率为315kW～10000kW的完美无谐波高压变频器（PERFECTHARMONY），无需附加输出变压器实现了直接3kV或6kV高压输出；首家在高压变频器中采用了先进的IGBT开关器件；达到了完美的输入输出波形，无需附加任何滤波器就可以满足各国供电部门对谐波的严格要求；输入功率因数达到095以上；总体效率（包括输入隔离变压在内）高达97％。达到这样高指标的原因是因为采用了三项新的高压变频技术：一是在输出逆变器部分采用了具有独立电源单相桥式SPWM逆变器的直接串联叠加；二是在输入整流部分采用了多相多重叠加整流技术；三是在结构上采用了功率单元模块化技术。

2单相桥式SPWM逆变器的直接串联叠加

单相桥式SPWM逆变器的直接串联叠加法，是通过N个具有独立直流电源的单相桥式SPWM逆变器直接串联的方式级联而成的，这是专为高压大功率逆变器使用的一种串联叠加法。此法是用N个依次移开2π/N相位角的载波三角波，与同一个正弦调制波进行比较产生出N组控制信号，用这N组控制信号（N组信号依次相差2π/N相位角）去依次控制N个具有独立直流电源的单相桥式SPWM逆变器，使每一个单相桥式逆变器输出相同的基波电压，然后将N个单相桥式逆变器的输出电压串联起来，就可以得到多电平SPWM无谐波电压输出，这种串联不存在均压问题。

21两个单相桥式SPWM逆变器的串联叠加

现个具有独立直流电源单相桥式SPWM逆变器的直接串联叠加电路如图1所示。由于N=2，所以载波三角波的移相角α==π(=180°)。对于三相输出逆变器来说，其A相电路由两个单相桥式SPWM逆变器A1和A2串联组成。A1的载波三角波的移相角α=0；A2的载波三角波的移相角α=(=180°)。A1和A2的载波三角波用同一个A相的正弦波进行调制。这样就可以得到A1的输出电压up1、A2的输出电压up2。up1和up2具有相同的基波电压。A1和A2串联后的输出电压uA=up1＋up2就是输出为正弦波的无谐波电压、其波形如图2所示。

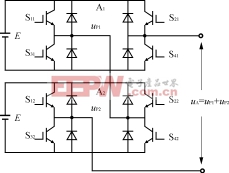
图1两个单相桥式SPWM逆变器的串联叠加

图2A1及A2串联叠加后的波形

为了求出单相桥式SPWM逆变器A1、A2的输出电压up1、up2的SPWM波形，必须先求出SPWM波形中各脉冲前、后沿a、b点的座标，为此先列出载波三角波的方程式：

对于单相逆变器A1α=0

（1）

对于单相逆变器A2α=180°（2）

K=0，±1，±2…

调制波的方程式为：us(t)=Ussinωst（3）假定载波比，调制比。

对于单相逆变器A2的输出电压up2的波形，

在采样点a：Ussinωst=－

令ωst=Y；ωct=X，

则X=2πK＋π－α－πMsinY

在采样点b：X=2πK＋π－α＋πMsinY

从图2中A2的up2波形可知：X=ωct在2πK＋α到2π(K＋1)＋α区间内，在a、b点之间得到up2的正脉冲，故可以得到up2的SPWM波的时间函数式为：up2(X，Y)=(4)Y=X

函数up2(X，Y)可以用双重付里叶级数表示：up2(X，Y)=Aoo＋(AoncosnY＋BonsinnY)＋(AmocosmX＋BmosinmY)＋{Amncos(mX＋nY)＋Bmnsin(mX＋nY)}

式中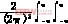：Amn＋jBmn=up2(X，Y)

将式（4）代入上式得：Amn＋jBmn==

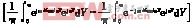由贝塞尔函数得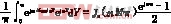：所以：Amn＋jBmn=

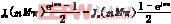·〔〕=j(5)

当n为零或偶数时，=0，Amn＋jBmn=0，

当n为奇数时，=2所以：Amn＋jBmn=jJn(mMπ)

·〔cosm(π－α)＋jsinm(π－α)〕Amn=－Jn(mMπ)sinm(π－α)；Bmn=Jn(mMπ)cosm(π－α)当m=0时=1Aon＋Bon=up2(X，Y)

因为up2(X，Y)是奇函数，故得：

Aon=0Bon=up2(X，Y)=

当n=1时，Bo1=ME；当n≠1时，Bon=0

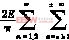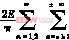
故得up2的SPWM波形的双重付里叶级数式为：up2(t)=MEsinωst＋cosm(π－α)·sin〔(mF＋n)ωst〕－sinm(π－α)

·cos〔(mF＋n)ωst〕(6)

由于A1的载波三角波的α=0；由于A2的载波三角波的α=π，A1和A2用的又是同一个正弦调制波，所以由式（6）可得：up1（t）=MEsinωst＋cosm(π－0)·sin〔(mF＋n)ωst〕－sinm(π－0)

cos〔(mF＋n)ωst〕(7)up2（t）=MEsinωst＋cosm(π－π)·sin〔(mF＋n)ωst〕－sinm(π－π)

·cos〔(mF＋n)ωst〕(8)

由于up1（t）和up2（t）的基波电压相同；同时又有sinm(π－0)＋sinm(π－π)=0。对于cosm(π－0)＋coom(π－π)：当m等于偶数时等于2；当m为奇数时等于零，所以式（7）和式（8）相加得到的uA的双重付里叶级数式为：uA=up1（t）＋up2（t）=2MEsinωst＋sin〔(mF＋n)ωst〕(9)