电压源高频交流环节AC AC变换器原理研究

摘要：首次提出了电压源高频交流环节AC/AC变换器电路拓扑族，这类电路拓扑由输入周波变换器、高频变压器、输出周波变换器构成。分析研究了这类变换器稳态原理与移相控制策略，绘出了变换器的外特性曲线。这类变换器具有电路拓扑简洁、两级功率变换(LFAC/HFAC/LFAC)、双向功率流、高频电气隔离、网侧电流波形可得到改善、负载适应能力强等优点。PSPICE仿真波形充分证实了这类变换器的正确性和先进性。关键词：AC/AC变换器；高频交流环节；周波变换器；电压源；移相控制ResearchonPrinciplesofVoltageMode

1引言

电力电子研究人员对DC/DC变换器、AC/DC变换器、DC/AC逆变器高频环节变换技术[1]的研究，已取得了显著的成果；对AC/AC变换技术的研究仅限于交流负载与交流电网无电气隔离的晶闸管相控变频器、矩阵变换器[2]。

本文首次提出并深入研究了交流负载与交流电网有高频电气隔离的基于Forward变换器的电压源高频交流环节AC/AC变换器，对电力电子学的发展和实现新型电子变压器、正弦交流稳压器均具有重要意义。

2电压源高频交流环节AC/AC变换器电路

拓扑族与控制原理

2．1电路结构与拓扑族

基于Forward变换器的电压源高频交流环节AC/AC变换器电路结构，如图1(a)所示。该电路结构由输入周波变换器、高频变压器、输出周波变换器构成，能够将一种正弦交流电变换成另一种同频率的正弦交流电。输入、输出周波变换器均由四象限功率开关(能承受双向电压应力和双向电流应力)构成。电压源高频交流环节AC/AC变换器电路拓扑族共8种，如图1(b)～(i)所示。

图1电压源高频交流环节AC/AC变换器电路结构与拓扑族

2．2控制原理

电压源高频交流环节AC/AC变换器采用移相

国家自然科学基金（59977010）、江苏省自然科学基金（BK99121）资助项目。

(a)电路结构

(b)单正激式(c)并联交错正激式

(d)推挽全波式(e)推挽桥式

(f)半桥全波式(g)半桥桥式

(h)全桥全波式(i)全桥桥式

控制策略，如图2所示。四象限功率开关S1(S1′)与S2(S2′)、S3(S3′)与S4(S4′)的驱动信号为互补的高频方波信号，但S3(S3′)与S1(S1′)、S4(S4′)与S2(S2′)之间的驱动信号均有相位差θ(0≤θ≤180°)。图2中，Ts=1/fs为开关周期，fs为开关频率，uAB为滤波器的前端电压。S3(S3′)与S1(S1′)、S4(S4′)与S2(S2′)之间在一个开关周期的共同导通时间DTs/2可表示为

DTs/2=Ts(180°－θ)/(2×180°)(1)

式中：D为占空比。

3电压源高频交流环节AC/AC变换器稳态

原理与外特性

3.1稳态原理

以全桥全波式电路拓扑为例，研究这类变换器的稳态原理与外特性，如图3(a)所示。该变换器稳态工作且CCM模式时，在一个开关周期Ts内可分为四个开关状态，其等效电路如图3(b)～(e)所示。

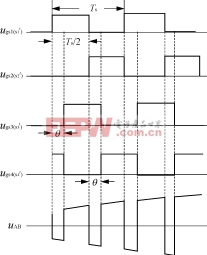
图2电压源高频交流环节AC/AC变换器移相控制原理

图3(b)、(d)和图3(c)、(e)可分别用图4(a)、(b)所示等效电路表示，其中r为包括变压器绕组等效电

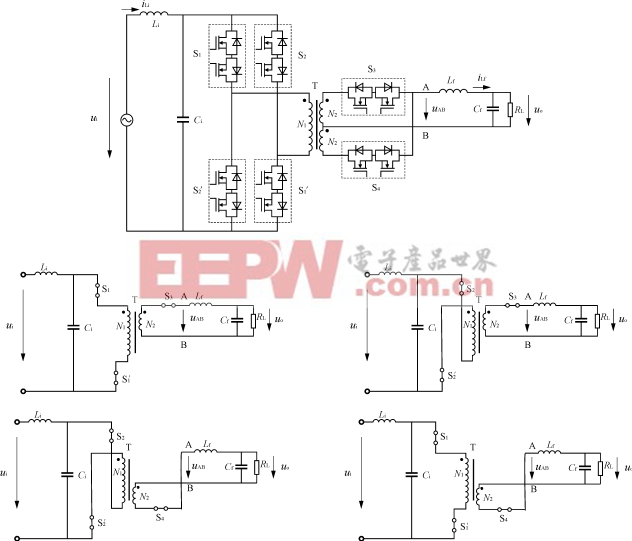
图3全桥全波式电压源高频交流环节AC/AC变换器及其CCM模式时开关状态电路

(a)全桥全波式电路拓扑

(b)S1(S1′)、S3导通，S2(S2′)、S4截止(c)S2(S2′)、S3导通，S1(S1′)、S4截止

(d)S2(S2′)、S4导通，S1(S1′)、S3截止(e)S1(S1′)、S4导通，S2(S2′)、S3截止

阻、功率开关通态电阻、滤波电感寄生电阻等在内的等效电阻。

由于开关频率fs远大于输出LC滤波器的截止频率和输入、输出正弦交流电压的频率，因此，在一个开关周期Ts内输入电压ui和输出电压uo均可看成恒定量，可用状态空间平均法建立输出电压与输入电压之间的关系式。

图4(a)所示等效电路的状态方程为Lf=－riLf＋ui－uo(2.a)Cf=iLf－(2.b)

图4(b)所示等效电路的状态方程为Lf=－riLf－ui－uo(3.a)Cf=iLf－(3.b)式(2)乘以D加式(3)乘以(1－D)，令=0，=0，可得状态变量在任何一个开关周期内的稳态值为ILf=(4.a)Uo=(4.b)

电压源高频交流环节AC/AC变换器原理研究

(a)S1(S1′)、S3或S2(S2′)、S4导通时

(b)S2(S2′)、S3或S1(S1′)、S4导通时

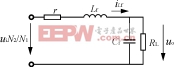
图4电压源高频交流环节AC/AC

变换器CCM模式时两种等效电路

(b)DCM模式

(a)临界CCM模式

图5滤波电感电流临界CCM和DCM

模式时一个开关周期内的波形

3.2稳态时变换器外特性

3.2.1理想情形(r=0)

由式(4.b)可知，理想情形且CCM模式时变换器的外特性为Uo=(5)

滤波电感电流临界连续和DCM模式时一个开关周期内的原理波形，如图5所示。

由图5(a)可知，t2－t1=DTs/2。t=t1～t2时，有uiN2/N1－uo=Lf=Lf=Lf(6)

电感