SPWM稳频稳压逆变电源
摘要:介绍了SPWM稳频稳压逆变电源的设计方案,重点分析了其测量系统,该电源设备通过取样电机实际响应电压Vpwm,解决了SPWM脉宽调制式变频器与电机的匹配问题。
关键词:逆变器;负载匹配;稳频稳压;测量系统
0 引言
近年来,变频器与变频电机组成的拖动系统在生产中发挥着重要的作用。然而在使用中经常发现变频器与变频电机不能很好地匹配,这个问题严重困扰着变频器及变频电机的生产厂家。因此有必要研发SPWM稳频稳压电源,使电源频率可调范围为0~500Hz,电压可调范围为0~420V(基波)。且能显示电机实际响应的SPWM波的电压(Vpwm)、电流、频率和功率等。这样,变频器的生产厂家就可以该电源为标准,测量出与之配套的变频电机真实使用的电压值、电流值、频率值,来调校变频器的矢量控制参数或v/f控制参数。而电机生产厂家也可根据该标准电源来调整电机的参数,使其与变频器匹配。
1 工作原理及测量系统分析
如图1所示,SPWM稳频稳压电源主电路与市面上成熟的SPWM逆变电源类似。当交流电机和一个脉宽调制变频器一起被用于变频调速时,设计Vpwm是为了测量交流电机有效电压。这种类型的变频器首先从交流源产生一个直流电压E,被称为直流链电压。然后利用电力电子变换技术,采用脉宽调制来变换直流链电压,可以得到一个三相电源系统,例如:通过IGBT在数ms内将直流电压开关数百次,来创建频率可调的三相电压。然而输出电压并不是正弦波,而是一个恒幅值的高频斩波波形,如图2所示。这种电压被送给电机,由于电机是一个大的感性负载,主要对电源电压低频部分作出响应,故电流波形仅具有少量的高频成分,近似为一个正弦波。对于系统设计者和使用者,能够测量出电机实际接收到的电压Vpwm,检查电机的矢量参数或v/f是否超出范围是非常重要的。如果长时间超出电机的标称v/f值(例如,电机在高频、低速下运转),电机将会发热,甚至损坏,而产生严重后果。然而需要注意的是,用电压表测量该斩波波形的电压是有效值Vrms,而电机响应的实际有效电压Vpwm与图2的脉宽调制波的有效值Vrms之间存在非常大的误差。例如某系统,当Vpwm=144V时,Vrms=192V,误差率为(192-144)/144=33.3%
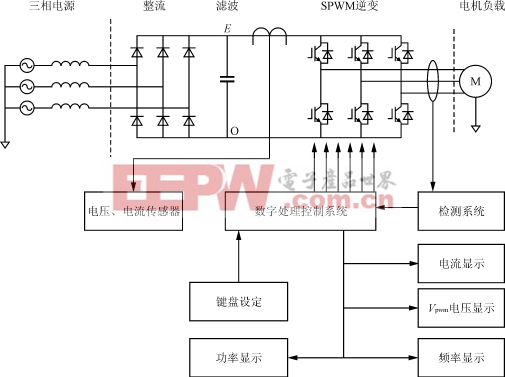
图1 测量系统原理框图
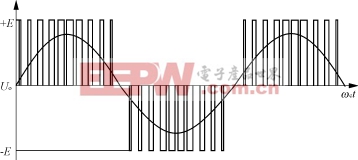
图2 SPWM波形与基波
采样经检测系统将数据送给控制系统。控制系统通过计算基频的整个周期的绝对平均电压的有效值即均方根值检测出VPWM。
例如,当载波比N=ωc/ωs取3的奇整倍数时,线电压uab的傅立叶级数表达式为
uab=![]() MEcos(ωst-
MEcos(ωst-![]() -φ)-
-φ)-![]()
 sin
sin![]() sin
sin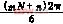
sin[(mN+n)(ωst-![]() )-
)-![]() -nφ](1)
-nφ](1)
式中:M为调制度;
m与n分别为相对于载波和调制波的谐波次数;
ωc,ωs分别为载波和调制波的角频率。
同样可推导出线电压ubc及uca的方程式。显然幅值很高的载波成分被消除掉了;载波谐波也被消除;它们的上下边频中的零序谐波成分也不存在了;上式中sin![]() 是消除m和n的同时为偶数或同时为奇数时的那些项。表1为uab中谐波的通用值。
是消除m和n的同时为偶数或同时为奇数时的那些项。表1为uab中谐波的通用值。
表1 uab中谐波的通用值
| km±n | M | ||||
|---|---|---|---|---|---|
| 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | |
| 1 | 0.122 | 0.245 | 0.267 | 0.490 | 0.612 |
| m±2 | 0.010 | 0.037 | 0.080 | 0.135 | 0.195 |
| m±4 | 0.005 | 0.011 | |||
| 2m±1 | 0.116 | 0.200 | 0.227 | 0.192 | 0.111 |
| 2m±5 | 0.008 | 0.020 | |||
| 3m±2 | 0.027 | 0.085 | 0.124 | 0.108 | 0.038 |
| 3m±4 | 0.007 | 0.029 | 0.064 | 0.096 | |
| 4m±1 | 0.100 | 0.096 | 0.005 | 0.064 | 0.042 |
| 4m±5 | 0.021 | 0.051 | 0.073 | ||
| 4m±7 | 0.010 | 0.030 | |||
图3所示的是在信号中存在高频成分时谐波和基波相迭加的情景。谐波的次数越高对平均值的影响越小。
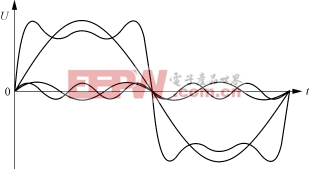
图3 基波、三次、五次谐波叠加
采用图1的测量系统,取输出信号的基频和测量基频的整数个周期,将有关数据传送给控制系统,控制系统通过计算基频波的均方根值(有效值),最终显示出电机实际响应的Vpwm值。
2 稳压稳频系统设计方法
在稳频稳压SPWM电源设计前必须明确系统要求的技术指标,根据这些指标进行系统的静态和动态设计,从而明确各单元电路应达到的主要技术指标。合理地分给各个单元,然后进行参数计算。正确的参数被送给数字电路进行程序设计来控制频率与电压。由图4稳幅原理框图,得到图5闭环系统结构图。
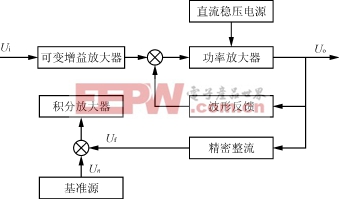
图4 稳幅原理框图
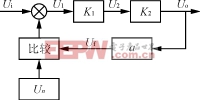
图5闭环系统结构框图
2.1 静态设计
由图5可推导出静态特征方程
Uo=KUnUi/(1+αK1K2Ui)(2)
则静态结构图如图6所示。

图6 静态结构图
根据静态特征方程和系统的技术指标,可确定各单元电路的技术指
- 中小功率光伏用逆变电源现状发展分析(12-09)
- 一款基于UC2525的交流逆变电源设计(12-08)
- 弧焊逆变电源的谐波分析和抑制(12-08)
- 逆变电源及逆变电源的原理(12-08)
- 逆变电源的SPWM波形发生电路(12-08)
- 关于纯逆变电源逆变器的介绍(12-08)
