flyback的分析和设计

大家最早可能接触,也是可能接触最多的电路拓扑应该是flyback.至少我刚刚接触电源的时候,最先就是flyback.不会设计,连分析也不懂,唯一能做的是模仿(额,难听点就是抄袭了:( ).这样子的状态持续了一段时间后,才开始慢慢的有一些了解.为了让初学者能更快的上手,少走弯路,于是有了这一章.

为了分析flyback电路,我们从flyback的源头开始说吧.Flyback是从最基本的三种电路中的buck-boost演变而来的.所以对buck-boost的分析,一定有助于对flyback的分析,而且buck-boost看起来似乎要比flyback简单,至少它没有变压器吧.

为了证明我没有骗你,下面将要开始来对buck-boost进行演变,最终会演变成flyback.

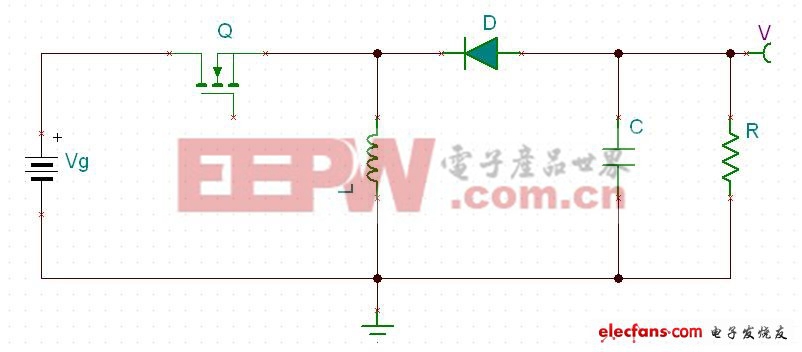
图一

图一 是buck-boost的原型电路. 把电感L绕一个并联线圈出来,如图二:

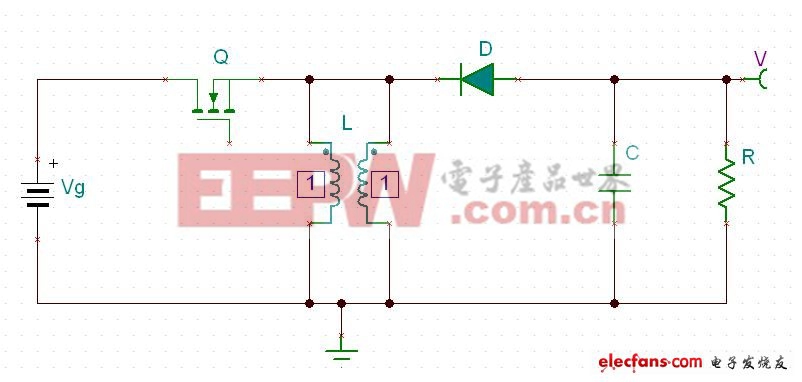
图二

把L的2个并联线圈断开连接,并且改变圈数比,改为:1:n,如图三:

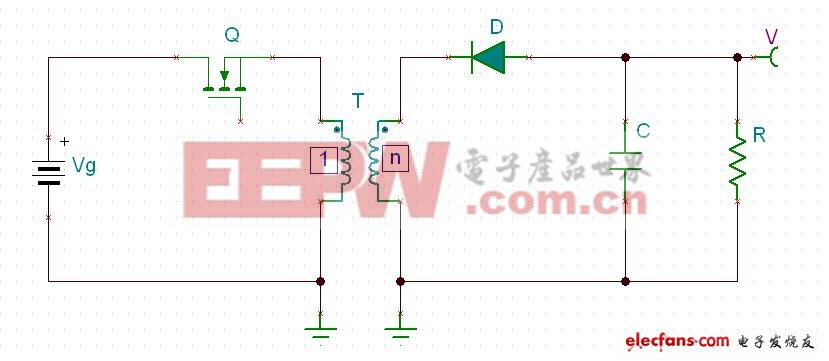
图三

把图三中的二极管沿着所在回路移动,变成阴极朝外的样子,并且,改变输出电压V和接地的位置如图四:

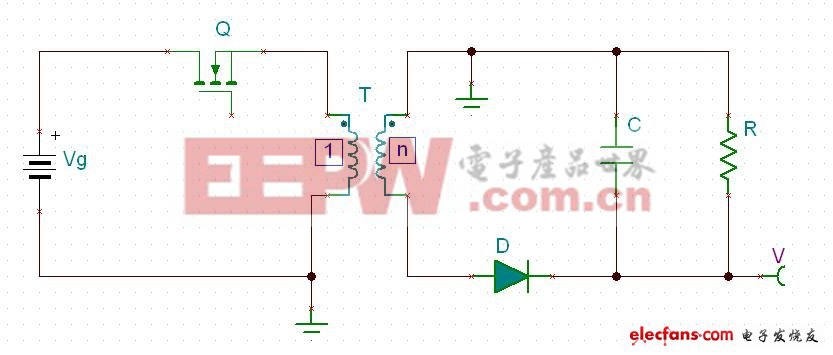
图四

把图四中的Q顺着回路移动到变压器下方,如图五:

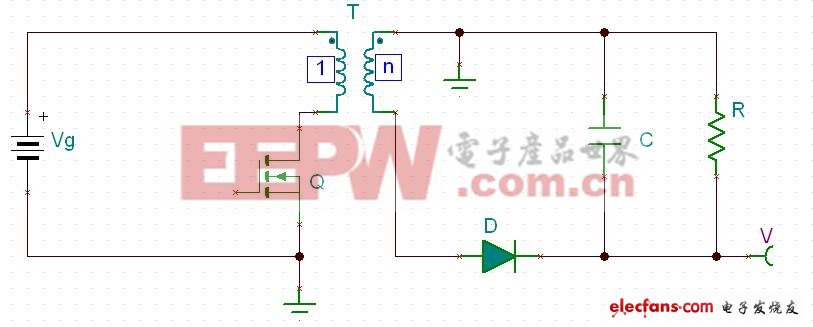
图五

把图五的电路,重新整理一下成图六.^_^,这样子和你见到的flyback有点像了吧.

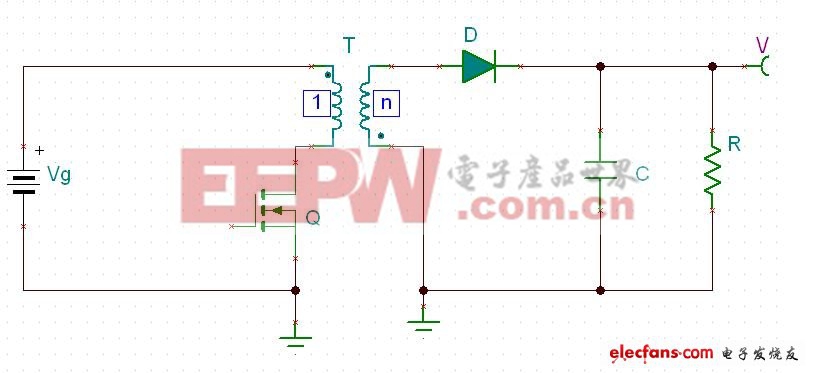
图六

以上说明,我们研究buck-boost的行为特性,对研究flyback的行为特性有很大的帮助.

1. 电路工作在连续状态(CCM),也就是说电感电流L是连续的,任何时候电感中总存在电流.(电路的另一种工作状态DCM将在以后的章节中分析)

2. 在一的假设下,电路工作就可以分成2个状态,状态1,Q开通,二极管D关断,这个状态时间长度为t1, ,Ts为周期,这个状态记为d,状态2,Q关断,二极管D开通,这个状态记为 ,d' ＝1-d.

3. 电感L中的电流 纹波和电容C上的电压纹波相对其直流分流来说都很小.一个好的设计,要求输出的电压纹波总是很小,所以,C的纹波小,总是成立的.

4. 所有的损耗都不讨论先.即,电路所有原件是理想的.

5. 电路工作在一个稳定的状态下.第一个工作状态:mosfet Q开通,二极管D关断.如图八所示:

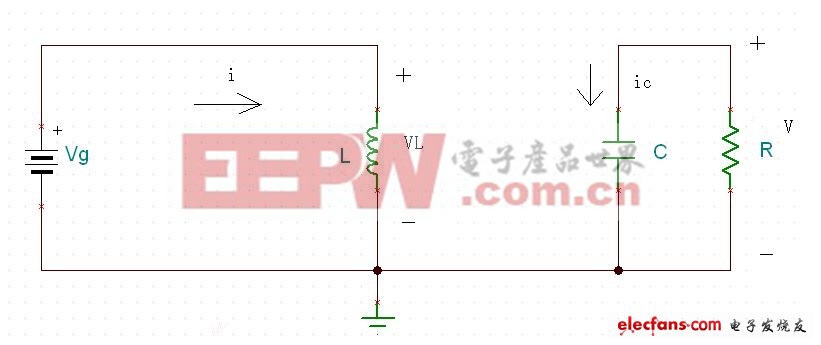
图八

列写状态方程: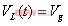
(1)
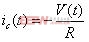(2)
因为有前面的假设,所以2可以简化为: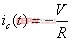
(3)
状态1的持续时间为 dTs.

第二个工作状态:Mosfet Q关断,二极管D开通.如图九所示:

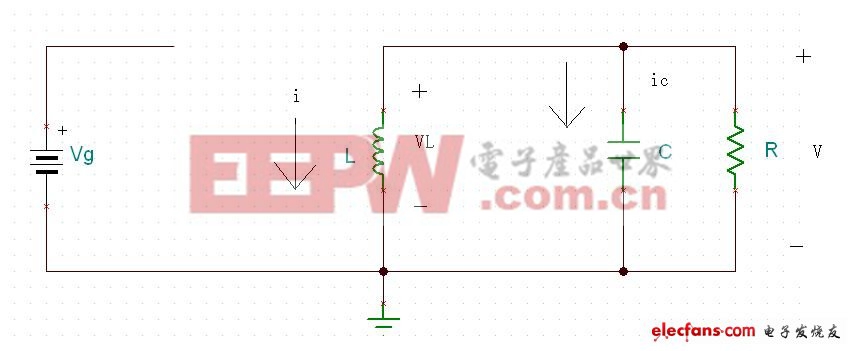
图九

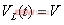(4)
(5)
状态2持续时间为(1-d)Ts,记为d'Ts.

由于这是一个和谐的电路,所以有: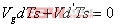
(6)
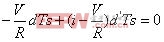(7)
解等式 6 和 7 ,并利用 d+d' =1可得: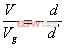
(8)
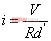(9)
从等式 8 看到了在CCM模式下面buck-boost的直流增益,因为flyback是从buck-boost变来的,所以我们猜测flyback的直流增益应该和这个有些像(具体见后文推导).

从等式 9 看到了在CCM模式下面buck-boost的电感的平均电流就等于输出的电流除以d'.接着马上研究一下mosfet和D所承受的电压.

在状态1,二极管D关断,所承受的反压为: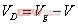
(10)
利用等式8的结果,则(10)可以写为: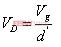 (11)
同理可在状态 2 计算Mosfet所承受的电压: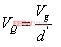(12)

等式 11 和等式 12 在告诉我们,占空比 d 越大,输出电压V的值越高,Mosfet和二极管D所承受的电压越高(好像是废话,输出电压越高,直观来说器件所承受的电压也越高嘛).等式 11 和等式 12,不仅仅验证了这个直观的想法,而且定量的给出了电压的大小,这个是有意义的事情.

下面研究一下这个电路中的电流吧.

电感的平均电流i等式9 已经给出,是和输出电流相关,那电感的纹波电流呢?

在状态1,电感电流的示意图如图十所示(在画图板里面画的图,难看一点了,能看明白就好了,将就用下吧):

图十

从图十中计算: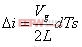
(13)
这个的大小是可以被设计的.而且,如果电路是理想无损耗的话,当输入电压和输出电压确定后,这个值是不随着输出电流变化的,它被电感所确定了!这个很重要,对后面的DCM状态的分析很重要.前面有假设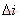相对i很小,那现在给出一个具体的值,比如 设计成i的5%.

有效值(RMS)的计算,按照公式是这么算: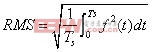
(14)

在电源中,最常见的是梯形波(三角波是梯形波的一种特殊形式),每次都按 14 的方法计算RMS值是不是觉得很烦呢?有没有简单的方法啊?答案,有,下面就是一个很简单的计算诸如梯形波一类分段线性函数的有效值的方法.真的很简单,像梯形波这样子,一般用心算就可以得出来近似值了哦...

一个如图十一的波形,有效值可以这样子计算:

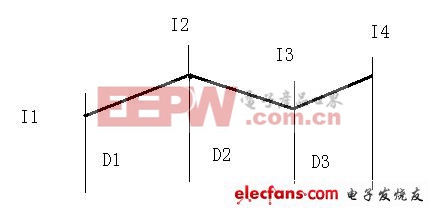图十一

(14a)

其中D1,D2,D3,分别表示该段经历的时间占总时间的比例.

好,马上来利用一下我们的秘籍来计算通过Mosfet,二极管D和电感的RMS电流.这个事情很有意义.

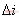已经假设为5%的i的大小,则通过Mosfet的RMS电流
(15)
有发现什么没有?这个值是不是非常接近于用电感电流的平均值i来计算的RMS值啊(说明在小纹波的情况下,用平均值来代替RMS值,是一个好办法.因为通常来说,平均值都比RMS值好计算^_^).

同理,流过二极管D的RMS电流可以表示为: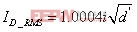
(16)
流过电感L的RMS电流可以表示为: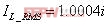
(17)

到这里,几乎所有