基于PID单相逆变器复合控制方案设计

　　PID控制作为一种经典控制算法，具有结构简单、易于调试、动态响应特性快、鲁棒性强等特点。但是，对于中、低频周期信号，该算法仍无法实现无静差控制；对由非线性负载引起的输出波形畸变的调节能力也较差。

　　本文介绍了一种PID控制器与重复控制器采用串联拓扑结构的方案，将稳定的PID+控制对象闭环系统作为重复控制器的控制对象，在保证系统稳态误差和动态性能的同时，简化了重复控制器的设计。

　　1 逆变器模型

　　式中，u0为输出电压；i 为电感电流； 为负载电阻；C为滤波器电容；￡为电容等效串联电阻：

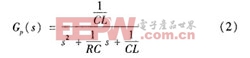
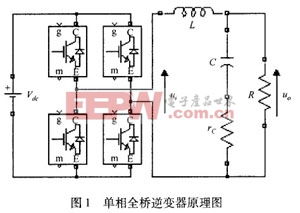
　　取采样频率和开关频率相等，把逆变桥看作一个零阶保持器，将式（2）离散化可得对象的脉冲传递函数为：

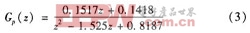
2 PID控制器设计

　　图2所示为PID控制系统的开环频率特性图（Bode图）。其中，G0为被控对象；G 为PID控制器；G=Gp×G0

　　按照传统PID设计理论，首先设开环系数为K=200，目的是提高系统低频增益，减小稳态误差。但是K值过大会降低系统稳定性，所以在低频段 处加一零点，与积分环节构成滞后校正。该滞后环节的作用主要有两条：一是在保证系统暂态性能基本不变的情况下，提高系统低频响应的增益，减小系统的稳态误差；二是利用其低通滤波特性衰减系统高频响应增益，提高系统的相角裕度，以改善系统的稳定性。

　　在中频段60 处加一零点，同时在高频段 处加一极点，由此构成超前校正。其作用主要有两条：一是利用相角超前特性增大系统的相角裕度，提高系统的截止频率，保证系统快速的动态响应；二是衰减系统高频响应增益，抑制高频噪声，提高系统鲁棒性。

　　图2中G为PID控制系统开环传递函数，由其频率特性曲线可以看到，系统低频开环增益非常大；截止频率附近频段相角裕度增大；高频段开环增益很小，抑制了高频干扰信号。通过滞后一超前相校正方法对PID控制器进行设计，达到了预期的目的。经过以上分析，PID传递函数为：

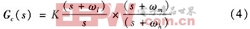
　　取采样频率和开关频率相等，采用零阶保持器将式（4）离散化可得对象的脉冲传递函数：

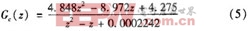
3 重复控制器设计

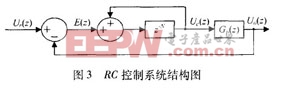
　　根据内模原理，在闭环系统中加入外部周期信号动态模型，则系统可以达到对外部周期信号渐近跟踪的目的，重复控制策略正是基于这一原理。图3为基本重复控制器系统结构图，其中重复控制器离散表达式为：

　　式中，Ⅳ为每基波周期对输出电压的采样次数。

　　由式（6）可知，当频率为∞=2~k/T（K=0，1，2，……，T为基波周期），由于z=1，所以若在闭环系统中嵌入重复控制器，将使开环增益趋向无穷大。在这种情况下，非谐波输入信号将被强烈衰减，达到精确跟踪输入信号的目的。但是，由于无法精确知道控制对象动态特性，所以开环增益趋向无穷大将恶化闭环系统的稳定性。为了保证系统稳定性，需对基本重复控制系统改进。

　　本方案提出的复合重复控制系统结构图如图4所示。

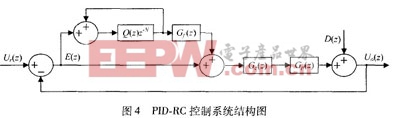
　　Q（z）、G，（。）为低通滤波补偿器，是重复控制器设计工作的重点。P（ ）的作用是将开环增益调节至很大的有限值，在不影响稳态精度的前提下保证系统稳定性；G，（ ）的作用是通过限制重复控制器的频带范围来提高系统的鲁棒性 。由图可得到系统的误差传递函数为：

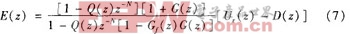
　　式中，

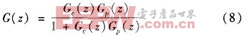
根据小增益定理，上述系统稳定的条件是：

　　① 闭环系统G（ ）是稳定的。

　　②

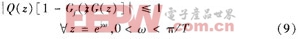
　　由误差传递函数式（7）可知，如果：

　　则式（7）可重列为：

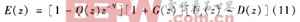
　　如果通过构造Q（z），在频率∞=2,rrk/T（k=0，1，2，……）处使：

　　则可以得到E（z）：0。所以，当系统满足式（10），式（12）时，各阶谐波的稳态误差理论上将趋向零。但是，由于实际的系统为非理想系统，上述设计要求无法满足所有频段的谐波，通常是在一定频率范围内，根据稳定性条件式（8）、式（9）和控制器条件式（10），式（12）设计重复控制器，满足系统对稳态和动态的要求。

　　根据式（8）、式（10），补偿器G，（ ）可以直接设计为G（ ）的逆函数。但是，如果G（z）是非最小相位系统，虽然式（10）仍成立，外部表现稳定，由于有不稳定零极点对消情况，这将导致系统内部不稳定。这种情况下，必须采用其他类型的补偿器对G，（ ）进行设计。

　　本文中提出的方案，控制对象是PID控制器镇定的稳定闭环系统，其本身即为最小相位系统，所以可以直接使用逆函数设计补偿器，即：

　　式（12）理论上要求p（z）=1；然而式（9）表明，由于高频段G（z）趋向0，Q（z）在高频段应小于1，所以Q（z）应是一个具有零相移的低通滤波器，其表达式为：

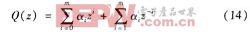
　　实际应用中，采用一阶低通滤波器完全可以满足系统要求：

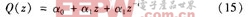
　　通过以上分析，现在重复控制器的两个滤波器可以根据式（13）、式（15）设计。

为了进一步理解重复控制器在系统中的作用，可以比