数字信号在不同时钟域间同步电路的设计
摘要:文中从控制信号和数据通路两个方面入手,设计了信号在不同时钟域之间的同步电路。采用直接锁存法和锁存反馈法来控制信号的跨时钟域传递,电路简洁、高效;采用异步FIFO (First In First Out)实现数据信号的同步,并通过格雷码和两级锁存来进行指针的跨时钟域传递,FIFO缓冲区的空满判断采用修改后的格雷码,对n+1位的编码可以节省(n2-n-2)/2次异或操作。该设计解决了信号跨时钟域传递时可能出现的亚稳态问题。
关键词:同步电路;异步FIFO;格雷码;亚稳态
随着系统应用需求的不断增多和集成电路技术的快速发展,大规模数字电路中常包含多个时钟域,设计中不可避免地要完成数字信号在不同时钟域间的传递,这时,如何保持系统的稳定,顺利完成控制信号和数据通路的传输就变得至关重要,这也是电路设计中最为棘手的问题之一。如果不采取一定的措施,控制信号和数据通路的接收方极易产生亚稳态信号,从而造成电路的同步出错。本文讨论了控制信号和数据通路的同步,提出了解决方案。
1 控制信号的同步技术
控制信号的同步分从快时钟域到慢时钟域、从慢时钟域到快时钟域的转换和异步输入控制信号的同步三种情况。分别采用直接锁存法和锁存反馈法来实现。
1.1 直接锁存法
控制信号从慢时钟域到快时钟域转换时,由于控制信号的有效宽度为慢时钟域周期,需要做特殊处理,保证跨时钟域后有效宽度为一个快时钟周期,否则信号转换到快时钟域后可能被误解释为连续的多个控制信号。同步电路如图1所示,在快时钟域对控制信号进行两级锁存,由于第二和第三个触发器的输出延迟一个快时钟周期,将它们做一个逻辑运算,就可以得到有效一个快时钟周期的控制信号。
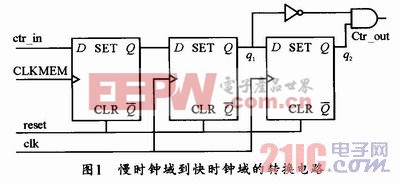
1.2 锁存反馈法
锁定反馈法主要解决信号从快时钟域向慢时钟域过渡时,如果信号宽度不满一个慢时钟周期,慢时钟可无法对信号进行正确采样的问题,也可用于处理异步输入信号的同步。如图2所示,同步装置由三级触发器组成,第一级触发器,数据输入端为电源,时钟输入端为控制信号,随后两级触发器由接收方时钟触发。发送方时钟域的控制信号到达后,第一级触发器的输出为高电平,在接收方时钟域对信号进行两级锁存后,若第三级触发器输出为高电平,就将第一级触发器清零。由于二三级触发器的输出延迟一个慢时钟周期,将它们做一个逻辑运算,就可以得到有效一个接收方时钟周期的控制信号。

图1、图2所示的电路,在接收方的时钟域采用两级触发器,大大增加了同步器的平均失效时间MTF(mean time to failure),MTF的有关计算公式在文献中给出。计算表明,对于大多数的应用,两级锁存器同步失效的概率很小,足以消除可能出现的亚稳态情况。
2 数据通路的同步
数据在不同时钟域之间的传递,一般不采用上述的同步器,因为多位数据的同时变化会使同步器的采样错误率大大增加。本文采用异步FIFO实现数据通路的同步。
2.1 异步FIFO
异步FIFO是一种先进先出的电路,发送方时钟域先把数据存储到RAM,稳定后再读取到接受方时钟域,从而实现异步数据的可靠传输。一般由读、写电路和FIFO存储体组成,如图3所示。

异步FIFO的设计主要有两个难点,一是如何实现两种异步信号的同步化问题以及如何消除由此产生的压稳态,二是如何正确的判断存储器空和满的状态。
为了提高FIFO的利用率,本文把FIFO组织成环形队列的形式。写指针始终指向下一个要写的字,读指针始终指向下一个要读的字。为了方便判断双端口存储器的空满/状态,给读写指针的最高位增加一个冗余位,把读写指针定义为[log2N:0],只有后log2N位是存储器地址。当FIFO第一次被完全写满的时候,写指针的值为N,而不是全零,所以可以根据读写指针方便的判断存储器的空满。当读写地址的存储器地址和冗余位都相等时,说明读指针追赶上写指针,即可认为FIFO为空:当存储器地址相等而冗余位不相等,即可认为FIFO是满的。
在异步FIFO的设计中,读写指针是在不同的时钟域里面产生的,只有同步到一个时钟域里才能进行比较。然而,把一个二进制计数器同步到另外一个时钟域里会面临很大的困难。这是因为自然二进制计数器的序列中一半的加1操作需要两个或者更多的计数器位的翻转。由于电路的固有延迟等原因,这些数据位的翻转不一定同时进行,那么就有可能在不同时钟域之间造成同步出错,从而导致读写指针的比较结果出错。
2.2 用格雷码实现读写指针
有效的解决指针跨时钟域传递的一个方法是格雷码技术,格雷码的特点是相邻的两个编码之间只有1位不同,消除了在同一个时钟沿多位编码同时变化所带来的问题。格雷码由二进制自然码右移一位后与原二进制码进行异或操作得到,运算关系为:
其中,N为n+1位二进制自然码,G为n+1位格雷码。
格雷码到二进制码的转变关系为: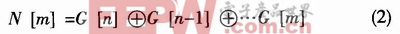
其中,N[m]为二进制码的第m位,G[m]为格雷码的第m位。
格雷码和自然码的对应关系示例如图4所示,可以看出,直接采用格雷码进行空满判断有些不方便,n+1位格雷码的上下半区是一个对称的结构,因为当写指针追赶上读指针时,读写指针的G[n-1:0]并不相等,无法进行满判断。本文采用修改后的编码,如图4所示,修改后的格雷码MG[n-1:0]上下半区是一个相等的结构,修改后的编码只有第n-1位和格雷码不同,第n-1位按如下方式产生: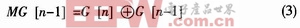
其中,MG[n-1]为格雷码的第n位,MG[n-1]为修改后的编码的第n-1位。
需要注意的是,修改后的编码最坏情况下,相邻的两个编码有两位不同,因此在跨时钟域的时候仍然采用格雷码,只有在跨时钟域结束后,进行空满判断的时候才对格雷码作修改。采用修改后的格雷码进行空满判断,比将格雷码转换到自然二进制进行判断节省运算量。例如,n+1位的格雷码转换到自然二进制码时,需要(n2+n)/2次异或操作,而转换为修改后的格雷码,只需n+1次异或操作,节省(n2-n-2)/2次异或操作(n>1)。
3 结束语
信号在不同时钟域之间的转换是复杂数字电路设计中不可缺少的一部分,直接锁存法和锁存反馈法可处理控制信号的同步,异步FIFO在跨时钟的数据交换方面具有高效的优势,本文设计的修改后的格雷码可以节省运算量,在具体设计时,需要在编码方法、跨时钟域的信号同步等关键问题上谨慎处理。
- 电源设计小贴士 1:为您的电源选择正确的工作频率(12-25)
- 用于电压或电流调节的新调节器架构(07-19)
- 超低静态电流电源管理IC延长便携应用工作时间(04-14)
- 电源设计小贴士 2:驾驭噪声电源(01-01)
- 负载点降压稳压器及其稳定性检查方法(07-19)
- 电源设计小贴士 3:阻尼输入滤波器(第一部分)(01-16)
