DC-DC变换器非线性混沌现象研究

：

。其中D是功率开关管的占空比，

和

分别是变换器的输入电压和输出电压。根据上述迭代式，用计算机仿真得出系统主要变量的相图，显示了系统由倍周期分岔通向混沌的道路。
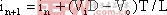
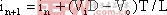
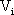
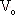
　　随后Deane和Hamill研究了电压型PWM Buck变换器负载并联电容足够大情况下的混沌现象[2]。通过解析的方法得到以下迭代式：

（1）
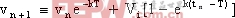
　　其中

可根据方程：

确定。该方程是超越方程，无法求解。系统是否稳定要根据相图的梯度确定的。结论是为了使该系统稳定运行，必须保证

时，

；

时，

，其中

，

是三角波电压，v是输出电压，

是参考电压，A是反馈系数。据此条件可以确定系统稳定运行的输入电压

的范围，若超出参数范围，系统运行中会出现多脉冲现象。
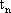
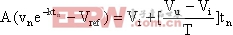
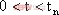
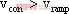
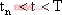
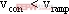
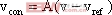
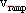
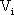
　　以上对一阶DC－DC变换器混沌模型的研究，都是在某些假定条件下进行的，因而与实际情况尚有一定差异。

3.1.2 二阶系统

　　当Buck和Boost变换器工作于连续模态，同时电容C不可忽略时，DC-DC变换器数学模型就要用二阶状态方程表示，所以称之为二阶DC－DC变换器系统。此时该数学模型更接近实际的DC-DC变换器，但是系统的分析比一阶系统困难，一般无法用解析的方法，只能用数值方法进行分析。Fossas和Oliver给出了电压型buck变换器周期1和周期2轨道的数学分析，描述了变换器运行中存在的次谐波、分岔和奇怪吸引子，并对其进行了数值分析。其它一些文献则采用频闪映射的方法进行研究。频闪映射是最常用的一种相图法，除此之外还有同步切换映射、异步切换映射和成对切换映射。使用相图法可以很直观的定性说明变换器运行的特性，是Buck和Boost变换器二阶系统研究可以采用的方法，但目前尚没有广泛的应用，为进一步推广这些相图分析方法，以下将分别加以介绍。
　　(1)　频闪映射
　　频闪映射是通过在每个锯齿波周期开始时刻对系统轨迹取样，得到一系列离散的点而获得的。其主要思想是确定一个初值，以此初值为变量求解下一周期的解，如此不断反复，最终得到所需精度的解f (n+1)。因此只要求得f (n+1)与f (n)之间的关系式，就能确定DC－DC功率变换器运行的发展状况，可以采用bisection法或牛顿－拉夫逊法等不同的迭代法获得f(n+1)。频闪映射虽然因为直观和构造方便而得到了广泛的应用，但在开关周期T的整数倍时刻，变换器可能没有相位切换，而出现周期跳跃的现象，这时频闪映射不能正确的加以区别，采用同步切换映射的方法可以解决这个问题。
　　(2) 同步切换映射
　　在开关切换周期T整数倍时刻对状态向量采样得到同步切换映射。以k表示采样时刻，则同步切换映射可以写为如下形式：

（2）
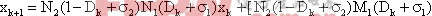
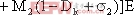
　　其中

和

表示

和

时刻之间相应状态的跳跃周期的数目。因为在发生周期跳跃现象时不对变量采样，所以可以解决频闪映射不能区别跳跃周期的问题。实际上，当

和

都为零时，同步切换映射就是频闪映射。
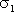
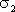
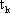
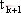
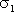
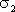
　　(3) 异步切换映射
　　连续模态的PWM DC－DC变换器开关状态的转换可以用方程：

的解来表示，其中

和

是反馈系数。此方程的解中，不是周期T的整数倍的解定义为异步切换时刻。所谓异步切换映射就是一对异步切换时刻和与之对应的状态变量，与下一对异步切换瞬间和与之对应的状态变量之间的关系：

，m表示第m个异步开关时刻。这种离散映射法也适用于其它所有的基本拓扑。
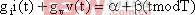
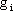
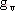
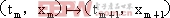
　　(4) 成对切换映射
　　成对切换映射在描述多脉冲行为时有良好的效果。多脉冲就是在一个周期内出现几次开关切换的现象。不管变换器的工作状态如何，系统总是从状态2（或1）切换到状态1（或2），然后又到状态2（或1），如此反复。若定义

为从状态1转换到状态2的时刻，并以此为初始时刻，则系统保持状态2到时刻

；在时刻

到时刻

系统保持状态1。因此可以认为系统状态是按照“状态2－状态1”或是“状态1－状态2”的序列进行切换的。设

，可得：

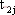
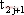
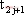
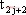
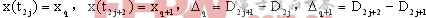
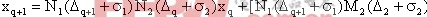
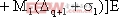
　　假设

，则由上式可得到异步切换映射。
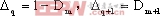
　　成对切换映射可以认为是分析二阶变换系统的最普通的映射，其基本的映射是唯一的。

3．2分析方法

　　DC-DC变换器混沌现象是一种复杂的非线性运动，具有自身特殊的动态特性，其研究需要借助一些特殊的非线性分析方法，下面介绍几种最常用也是最有效的方法。

3.2.1功率谱

　　混沌状态的特性之一是具有连续的宽带频谱，通过功率谱分析可以对混沌进行识别。但这种方法在实验过程中及自然状态下具有一定的局限性。因为实际条件下系统中存在的噪声会与混沌相混淆，所以连续宽带频谱只能作为混沌存在的必要条件，而非充分条件。而数值计算研究中因为不会引入外部噪声，所以可将连续宽带频谱作为混沌存在的一个判据。计算机上的快速傅立叶变换Fast Fourier Transform（FFT）和实时频谱分析仪的普及，使得功率谱分析变得简单易行。此方法已应用于DC-DC变换器的非线性现象研究，在数值研究及实验研究两方面均发挥了重要作用。

3.2.2庞加莱截面和分叉图截面和分叉图

　　基于离散映射可得到反映系统动态过程的庞加莱截面，以及由此衍生的奇怪吸引子[10,12,13]和分叉图。系统的混沌运动是一个复杂的动态过程，研究其相轨是及其困难的，需要构造庞加莱截面来研究。因为各种动态过程反映在庞加莱截面上的结构具有各自鲜明的特点，如周期运动对应为一个或有限个点，准周期运动对应一个环面，而混沌则对应具有一定结构的、在相空间占据有限范围的奇怪吸引子，于是就能很容易地区分不同的运动状态。分叉图是选择庞加莱截面的某个状态变量作为分叉图的其中一维坐标，另一维则是分叉参数。于是通过分叉图即可总览系统随参数变化而发生的动态特性的变化。

3.2.3 Lyapunov指数

　　动态系统的相邻轨道在系统演化过程中可以拉伸和压缩，其速率可能在相空间中各点不同，只有对运动轨迹各点的拉伸或压缩速率进行长期平均，才能刻画动态系统的整体效果，这就是Lyapunov指数的概念。正的Lyapunov指数刻画了混沌系统的主要特征，它表明：运动轨迹在每个局部都不稳定；相邻轨道以指数的速率分离；轨道在整体性的稳定因素（有界、耗散）作用下反复折叠，形成混沌吸引子。N维映射有n个拉伸或压缩方向，各方向分别对应一个Lyapunov指数。

[next]4 DC-DC变换器混沌发展方向及未来应用

4．1 混沌控制

　　DC-DC变换器混沌控制是一个新的概念和尝试，借助已发展起来的混沌控制方法如参数扰动法（特别是OGY方法）、纳入轨道和强迫迁徙方法、工程反馈控制方法以及智能控制方法等等，可以实现对DC-DC变换器混沌现象的消除、抑制或利用，已引起了非常广泛的注意和兴趣。
　　DC-DC变换器的混沌控制也取得了一定的成果。Roberto等人将OGY方法用于控制简单的一阶boost电路获得了成功，C.Batlle等人应用延迟反馈法来控制buck变换器，并得到控制参数的取值范围的解析条件。此外，Banerjee又提出了两种完全不同的控制方法：外加参数扰动法和开关切换控制法，对buck和boost变换器的成功控制说明了方法的可行性。DC-DC变换器的反混沌控制研究则尚处于起步阶段。

4．2 利用混沌功率谱特性提高电磁兼容性

　　DC/DC开关变换器最主要的电磁干扰源，来自其较高的工作频率（一般都达到几十kHz，最高可以达到几百kHz）和非线性的开关特性对周围的电磁环境的影响。此外开关变换器电路设计不当、元件选择不当以及结构布局或布线不合理都将造成的电磁干扰及使电磁干扰增大。
　　目前，抑制DC/DC开关变换器电磁干扰的措施，主要是采用附加硬件的技术，如利用金属或高分子材料屏蔽开关变换器电磁藕合辐射；利用电阻型、电介质型和磁介质型吸波材料将开关变换器所产生的电磁辐射能量转化为其它能量（主要是热能）而耗散掉；利用各种滤波器或用高功率因数整流器抑制开关变换器传导电磁干扰，以及利用接地、浮置、光电耦合、PCB板布线技术减少电磁干扰传播和发射。这些技术应用的最大缺点是增加开关变换器成本和体积，都没针对变换器的实际情况有根据开关变换器的特点，从机理上根本抑制开关变换器电磁干扰的产生。国外一些学者也试图从机理上解决功率开关变换器电磁干扰问题，如采用软开关技术减少功率开关管的开关电压、电流应力，改进功率开关变换器的PWM工作方式以减少高频电压电流的谐波，但仍然无法回避附加硬件、增加成本和体积的问题。
　　对电磁干扰特性的研究表明，若能使电磁干扰的能量均布在整个频谱范围，就能消弱电磁干扰的峰值，使DC/DC开关变换器电磁干扰得到抑制。非线性系统混沌特性研究表明，它具有连续频谱的特性，即在相同的电磁传输功率条件下，频谱平均分配在较宽的范围内，因此，混沌固有均布频谱的功能，可以利用混沌来提高DC/DC开关变换器的电磁兼容能力。显然，该种方法的优点在于无须外加设备，节约了成本。目前，虽然对DC/DC开关变换器混沌频谱特性还没有更深入的理解，但提供了应用混沌特性解决DC/DC开关变换器EMI的一个的研究思路，是一个值得探索的研究方向。

4．3 利用混沌同步特性进行均流控制

　　DC-DC变换器的并联均流一直是提高变换器容量、可靠性及降低成本的关键问题，采用混沌同步特性，可以使两个系统的输出特性保持一致，因而可以利用来实现DC-DC变换器的并联均流，其优点是成本低、均流特性好，无需附加其他硬件，只需在控制策略上加以改进。

4．4 利用混沌初值敏感性提高动态特性

　　混沌因为其对初值的敏感性，具有非混沌系统所没有的优越性。对混沌的系统，通过对其参数的微小改变就可以使其稳定于混沌吸引子中的某个周期轨道，或者使系统在不同的周期轨道间进行切换，这些周期轨道都是原系统运动方程的解，所以实现控制只需要很小的控制信号，即很小的能量，而无须改变系统的整体结构。但对于非混沌系统，小扰动只能轻微地改变系统的动力学。由于稳定的周期运动可塑性差，缺乏任意选择状态的灵活性，因此在设计系统时，让系统运行于混沌态（即反混沌）对取得易变性是非常有益的。近年来，反混沌控制开始成为一个研究热点。这方面的成功例子是美国国家航空和宇宙航行局National Aeronautics and Space Administration（NASA）的科学家们利用天体力学问题对扰动的敏感性，只用了少量的剩余肼燃料，在实现其主要任务后把太空船ISEE-31/C送到了距太阳8千万英里的地方，首次实现了与彗星的碰撞。
　　因而给DC-DC变换器动态响应的研究提供了一条新的思路。

[next]5 结论

　　对DC-DC变换器混沌现象研究仅仅是一个开始，还有许多问题尚待解决。但可以预计，随着对DC-DC变换器混沌现象研究的进一步深入，DC-DC变换器运动本质将被认识的更加深刻，DC-DC变换器的运行特性将在此基础上进一步提高，由此产生一些全新的DC-DC变换器设计技术和应用技术，使工业界受益。

参考文献

[1]J. H. B. Deane, D. C. Hamill, “Instability, subharmonics, and chaos in power electronic systems,” IEEE Trans. Power Electron., Vol. 5, No. 3, Jul. 1990, pp. 260-268.
[2] D. C. Hamill, J. H. B. Deane, and D. J. Jefferies, “Modeling of chaotic DC-DC converters by iterated nonlinear mappings,” IEEE Tran. Power Electron., Vol. 7, No. 1, Jan. 1992, pp. 25-36.
[3] M. di Bernardo, and F. Vasca, “Discrete-time maps for the analysis of bifurcations and chaos in DC/DC converters,” IEEE Trans. Circuits and Syst. I, Vol. 47, No. 2, Feb. 2000, pp. 130-142.
[4]C. K. Tse, and W. C. Y. Chan, “Chaos from a current-programmed #262;uk converter,” International Journal of Circuit Theory and Applications, Vol. 23, 1995, pp. 217-225.
[5] M. Alfayyoumi, A. H. Nayfeh, and D. Borojevic, “Modeling and analysis of switching-mode DC-DC regulators,” International Journal of Bifurcation and Chaos, Vol. 10, No. 2, 2000, pp. 373-390.
[6]M. D. Amore, et al., “A neural network approach for identification of EM field source:Analysis of PCB configuration,” in Proc. IEEE International Symposium on Electromagnetic Compatibility, Vol. 2, 1998, pp. 664-669.
[7] G. Antonini, et al., “EMC characterization of SMPS devices: circuit and radiated emissions model”, IEEE Trans, EMC, Vol.38, No.3, Aug. 1996, pp. 300-309.
[63] G. Venkataramanan, C. Chen, “An examination of radiated electromagnetic emission from hard and soft switched power converters”, in Proc. IEEE Industrial Application Conference(IAS’97),Vol. 2, 1997, pp. 1558-1563.
[8] F. Lin, D. Y. Chen, “Reduction of power supply EMI emission by switching frequency modulation”, IEEE Trans. Power Electron., Vol.9, No. 1, Jan. 1994, pp. 132-137.