逆变器基准信号几种产生方法的研究

1．引言

　　传统的逆变器控制电路都是采用模拟电路和小规模数字集成电路实现的。随着信息技术的发展，采用微处理器的数字控制技术已开始越来越多地应用于逆变电源。基于性能和成本的综合考虑，目前，部分数字化（即宽频带的电压调节器仍由模拟电路实现）不失为中小功率逆变器控制电路的优选方案。这种情况下，基准正弦信号首先由微处理器产生，变换成模拟信号后输出给模拟电压调节器。
　　基于微处理器产生的基准正弦信号频率和周期易于控制、调节精度高，可以满足逆变器并联运行等高性能控制的要求[1]。但同时时间和数值的量化必然造成谐波含量加大。本文将着重分析量化对几种正弦波产生方法的谐波影响。

2．数字化正弦波形产生的方法

　　软件产生正弦波常用的方法有两类：一类是表格＋D/A法。所谓表格就是在一个正弦波的周期中取N点，计算出每一段对应的幅值，形成一组数据，定时查表输出将数字量经过D/A转换形成阶梯波，滤波后成正弦波；另一类是正弦脉冲宽度调制（SPWM）法。数字正弦波数据经正三角波（有时也用锯齿波）软件调制，输出SPWM脉冲，再经模拟电路滤波解调成正弦波。

3．数字化正弦波的谐波分析

3.1 表格＋D/A法

　　我们在生成表格，即在数据处理的时候，常常会遇到时间量化的问题。将周期为T的正弦波由N个阶梯波近似，计算出的每一段对应的时间宽度并不一定是一个整数。设微处理器的定时时基为Ts，波形量化后，前N-1段中每一段对应的定时时间常数
　　k1=[T/(NTs)]　　　　 （1）
　　式中[]表示取整函数。为了保证整个周期为T不变，所以最后一段对应的时间常数
　　k2=[T/Ts]-k1(N-1)　　　（2）
　　不等于k1。即在整个阶梯波的末端会留有一段“时间尾巴”，而它的前N-1段则等份，显然这将造成波形的畸变，如图1所示。这一畸变造成的THD分析如下：

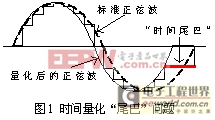
　　1) 不考虑时间量化的情况下，把正弦波时间轴一个周期2π直接等分成N段，每段对应的角度

=2π/N。由于正弦函数是一个奇函数，所以可以得到如图2所示的合成阶梯波（取N=120）。其函数表达式为：u=Umsin(n·2π/N)。因为u是奇函数，故其输出波形中没有偶次谐波而只有奇次谐波，所以它的傅里叶级数式中仅有正弦项。取第一段的中点为起始点（零点），对整个波形进行分段积分，即对一个周期2π内的每一段进行积分，由奇函数的性质，只要对半个周期0~π/2进行积分即可算得傅里叶级数如下：

　　 （3）
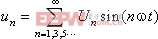
　　其中：

　（4）
　　式中[sin(k

)] 表示对sin(k

)的计算结果取整。
　　由计算知谐波含量主要分布在n = jN±1次。

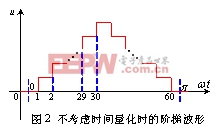
　　图3是在不考虑时间量化时合成阶梯波输出电压的频谱。根据总谐波畸变因素的公式算得当N取120，幅值为116时的THD 近似为1.5％。

　　2) 考虑时间量化的情况下，如图4为周期为20ms，N取120的合成阶梯波形。其函数表达式为：u=Umsin(n·[T/N]·2π/T )（[]表示取整函数）。由图4可知，它的傅里叶级数式中既有正弦项又有余弦项。同样取图4中第一段得中点为起始点，对整个波形分段
积分，求得傅立叶级数表达式如下：

　　（5）
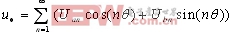
　　式中：

（6）

（7）
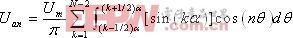
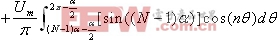
　　式中[sin(k

)]，[sin((N-1)

)] 表示分别对sin(k

)和sin((N-1)

)的计算结果取整。

　　由(6)和（7）式可求得谐波含量主要分布在n=j·N ，(j=1,2,3…)次周围。图5为取N=120，正弦波幅值为116时合成梯形波的频谱。

　　比较图3和图5可以看出，“尾巴”问题对谐波的次数没有影响，只是谐波幅值略微变化，并没有影响谐波畸变因素THD的值。经计算这种情况下的THD也大约为1.5％。

3.2 SPWM正弦脉宽调制法
　　SPWM法通常又有下面几种方法：载波为全波三角波（双极性）SPWM法、载波为半波三角波（单极性）SPWM法和“相位参差” SPWM法。下面以载波为全波三角波、起点在三角波的负脉冲处的单相三阶SPWM法为例来具体分析一下。
　　设幅值为Us，频率为fs的正弦调制波的方程式为：us=Ussin(ωst-ψ)，三角波用两个“分段线性函数”来表示，幅值为Uc ，频率为fc。“分段线性函数”的数学方程式为：

　
　　其中 k=0,1,2…。令调制度Us/Uc=M≤1,载波比ωs/ωc=fs/fc=N>>1,N任意正整数。
　　由于SPWM法调制在各个周期内所包含的脉冲模式没有重复性，所以我们不能以调制波的角频率ωs为基准，去使用一般分析傅里叶级数的方法分析，而是采用以载波的角频率ωc为基准，分析其边频带谐波分布情况的方法。这就是所谓的双重傅里叶级数法[2]。
　　经分析得其双重傅里叶级数表达式如下：

　（9）
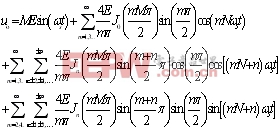
　　式中：E为输出波形的峰值。
　　由上面方程式可知，输出电压的谐波成分有：基波、载波与载波的m次谐波、载波及载波m次谐波的上下边频谐波。其中基波幅值为ME，谐波幅值为4EJn(mMπ/2)/(mπ)。在谐波次数（mN±n）中，当m为偶数时，载波的m次谐波，即不存在中心谐波；而当m为奇数时，载波的m次谐波，即中心谐波存在；当m＋n为偶数时，载波与载波的m次谐波的上下边频谐波也不存在；当m＋n为奇数时，载波与载波的m次谐波的上下边频谐波则存在。
　　表1列举了对于不同的M值由（9）式算所得的通用频谱数值。
表 1　对于大的N时，输出电压的谐波同用值