闭环反馈控制功率电子变换系统不稳定性抑制技术
时间:03-17
来源:互联网
点击:
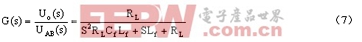
其有效阻尼比
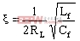
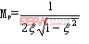
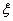
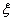
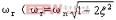

从滤波器瞬态响应角度看,在空载或轻载时,若LC滤波器前端出现一扰动阶跃输入Ur,则滤波器输出端相应地出现多次振荡,该振荡叠加到输出电压上,引起输出电压误差较大。为简化分析,在此仅讨论空载时情况,由叠加原理可得其振荡电路如图4b所示,Rd包括了引线电阻与感容寄生电阻,其值非常小。由该扰动阶跃输入Ur在滤波器输出端引起的振荡电压分量为
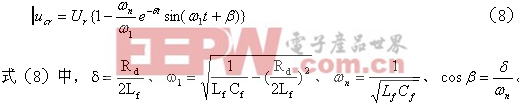
式(8)中第一项就此次扰动而言是个定值,它所引起的电压误差量通过反馈控制系统很容易得到调节;因为Rd非常小,故(8)式第二项幅值衰减很慢。虽然控制系统的补偿网络可对其进行一定的调节作用,但由于其频率ω1和无阻尼自然谐振频率ωn很接近,若控制系统补偿网络的动态响应速度不是非常迅速时(如电压单闭环反馈系统),则此时系统的调节作用就比较有限,并且反容易受到该振荡分量的影响,引起uAB中出现频率与无阻尼自然谐振频率ωn相近的谐波分量,LC输出滤波器不能对其进行有效抑制和滤除,最后表现为输出电压基波上叠加有一扰动振荡谐波分量。
对此,可从两个方面解决问题。一者可以通过调整控制系统补偿网络或控制策略,提高其动态响应速度来解决。例如让功率电子变换系统工作在DCM模式、或采用电流控制调制技术,使得输出滤波器由二阶降为一阶。这样对整个系统而言,LC滤波器对稳定性影响减小,从而加大系统稳定性[3]。但电流断续DCM工作模式只适用于功率较小的场合;电流调制技术较复杂,并且受控制策略的限制。
二者可以在不改变系统整体结构(如控制策略、工作模式等)的情况下加大 ,从而加快(8)式中第二项幅值的衰减,对其进行有效抑制。加大
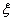
增加Rd有四种方法。一是在图4b Rd处串接一小电阻Rf(Rd与其相比很小可忽略不计),空载时其传递函数为
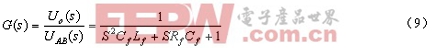
(9)式与(7)式空载时的传递函数相比,根轨迹的极点从虚轴向左半平面移动,增加了系统的稳定性;但这种方法在外接负载时流过小电阻Rf的电流很大,会产生过大的损耗。
第二种方法是在滤波电容Cf处并联一个较大的电阻RLS,经过计算推导,RLS折算成串联等效

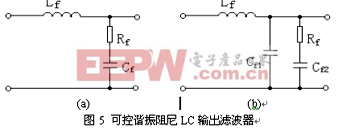
三是在Cf处串接一小电阻Rf,如图5a所示。这种方法避免了第一种方法在负载时损耗过大的缺点;在空载时第三种方法和第一种方法的电路结构虽然相同,但两者的传递函数并不一样,第三种方法的传递函数为
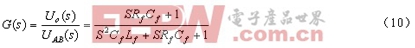
多了一个左半平面的零点,使得根轨迹向左移,增加了系统的稳定性,减小了系统响应的调整时间。但第三种方法会使输出电压中高频谐波滤除得不太干净,因为小电阻上有小部分高频谐波压降,另外在Cf较大时(结合基波频率时的容抗考虑)小电阻Rf上的损耗也不能忽视。
第四种方法是作者提出的可控谐振阻尼LC输出滤波器[7],如图5b所示。为了消除第三种方法的缺点,将Cf一分为二,其中一个电容串一小电阻Rf,Cf=Cf1+Cf2,Cf1会使输出电压中的高频谐波滤除干净,电阻Rf与Cf2相串可抑制振荡且使电阻损耗大为减小。Cf2值应尽可能取小以减小电阻Rd上的损耗,一般约为Cf的一半;电阻Rf一般取值几欧姆~几十欧姆左右,主要通过和Cf2的容抗比较而定,原则上Rf在远小于Cf2容抗的前提下尽可能取大但又必须保证其损耗要小,具体可通过计算、计算机仿真和试验综合确定。
4.2 仿真、试验结果与讨论
以一台1KVA 270VDC/115V400HzAC航空静止变流器为例,Lf=1mH,Cf=4uF,开关频率FS=50KHz,电压单闭环反馈控制,空载时传统无阻尼输出滤波器的输出电压仿真波形如图6a所示,uAB为滤波电感前端电压,uO为滤波器输出电压。可知滤波器的无阻尼自然振荡频率ωn=15811rad/s=2pfn=2p*2518,fn=2518Hz。图6a所示扰动谐波振荡频率约为400*15=6000Hz,约为2.4倍fn,这是因为闭环反馈控制环节的调节作用加快了扰动谐波的振荡频率。以一个无阻尼自然振荡周期Tn=1/fn时间内,式(8)中第二项幅值衰减到0.378倍(1/e)作为Rf的大致计算标准。则有公式
- 电源设计小贴士 1:为您的电源选择正确的工作频率(12-25)
- 用于电压或电流调节的新调节器架构(07-19)
- 超低静态电流电源管理IC延长便携应用工作时间(04-14)
- 电源设计小贴士 2:驾驭噪声电源(01-01)
- 负载点降压稳压器及其稳定性检查方法(07-19)
- 电源设计小贴士 3:阻尼输入滤波器(第一部分)(01-16)
