一种改进的频率选择表面等效电路模型

摘要：等效电路模型可以快速分析具有平行直线单元的频率选择表面，然而，现有的等效电路模型由于没有考虑介质厚度与相对介电常数的影响，在分析介质加载的频率选择表面时出现偏差。提出了一种方法，即将等效介电常数的概念引入到模型中，等效介电常数为介质厚度和相对介电常数的函数，采用曲线拟合确定该函数。通过仿真验证该模型在分析介质加载频率选择表面时精度较好。
关键词：频率选择表面；等效电路模型；曲线拟合；相对介电常数

频率选择表面(Frequency Selective Surface，FSS)的等效电路模型分析法是一种近似分析方法，可用于分析具有平行直线单元的FSS，如栅格单元、方环单元、双矩形环单元、基督十字单元等。等效电路模型的最大优点是算法简单、省时，可以在普通微型计算机上运行，有比较好的计算精度，物理意义明确，特别适用于工程设计。然而，现有的等效电路模型的经验公式中均不含介质厚度h和相对介电常数ε，所以，在分析有介质加载的FSS会出现偏差。为了解决这一问题，本文提出了一种曲线拟合与等效电路模型相结合的思路。
在等效电路模型基础上，首先修改模型中的等效介电常数εeff为介质厚度h与介质相对介电常数εr的二元函数。其次，通过对介质加载的FSS仿真，并与等效电路模型比较，反复修正εeff。最终得到εeff的较为精确的表达式，改进等效电路模型。

1 等效电路模型介绍
1．1 传统等效电路模型
现考虑以单一介质为衬底的单层FSS结构，FSS单元的上方为空气，下方为介质衬底，为了分析方便，可以把空气与介质衬底等效为一个相对介电常数为εeff的单一介质，εeff为等效介电常数。根据文献和文献，有等效电路经验公式如下所述：
(1)方环结构等效电路经验公式

然后根据LC回路以及传输线理论，就可以得到FSS的传输系数。可以看出，等效电路经验公式中不含介质厚度h和相对介电常数εr，却含有一个等效介电常数εeff，而εeff的取值没有固定的方法，为了完善等效电路经验公式，需要找出厚度h和相对介电常数εr与等效介电常数εeff之间的关系表达式：εeff=f(h，εr)。
1．2 改进的等效电路模型
首先，把相对介电常数εr设为定值，取不同的介质厚度h，用仿真软件对FSS进行仿真，得到传输特性曲线。根据谐振频点的值，通过经验公式编程求出这种情况下的等效介电常数εeff，因为每个厚度值h都与一个等效介电常数εeff对应，于是可以通过函数拟合得到等效介电常数εeff关于厚度h的表达式εeff(εr=const)=f(h)。改变相对介电常数εr，重复七面的步骤，于是每个相对介电常数εr值都能得到一个等效介电常数εeff关于厚度h的表达式，并且表达式的形式是一样的，具体形式为：，不同的只是表达式的系数a。由此可见，这个表达式的每个系数a随着相对介电常数εr的变化而变化，通过建立系数a与相对介电常数εr的对应表，可以拟合出系数a关于相对介电常数εr的函数an=an(εr)=knεr+dn，把每个系数都用相对介电常数来表示，然后代入到等效介电常数εeff关于厚度h的表达式εeff(εr=cons t)=f(h)中。最终得到了等效介电常数关于相对介电常数和厚度的函数。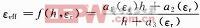将此函数代入到经验公式中，使得经验公式可以考虑相对介电常数和厚度的影响，从而完善了FSS的等效电路模型。

2 算例
2．1 方环
取方环尺寸为p=5．25 mm，s=0．47 mm，d=5．0 mm，g=0．25 mm的情况下进行仿真和编程，得到拟合函数如下：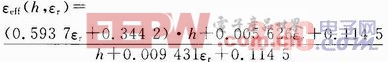

式中h的单位为mm。
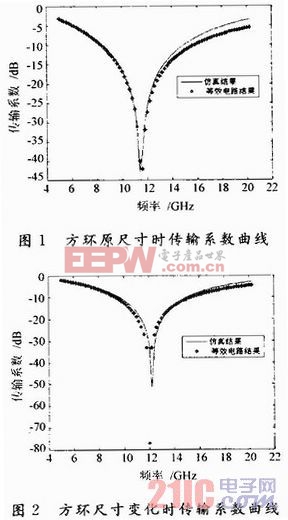
当厚度为0．4 mm，介电常数为3．5时有:εeff=f(0．4，3．5)=2．014 7，代入经验公式中。在原尺寸下，仿真结果与等效电路模型结果的传输系数曲线如图1所示。在尺寸变化为p=5．0 mm，s=0．28 mm，d=4．6 mm，g=0．4 mm时，仿真结果与等效电路模型结果的传输系数曲线如图2所示。

2．2 栅格
取栅格尺寸为p=27．0 mm，w1=0．2 mm，w2=3．5 mm，d=21．8 mm的情况下进行仿真和编程，得到拟合函数如下：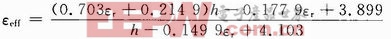

式中h的单位为mm。
当厚度为0．4 mm，介电常数为3．5时有：εeff=f(0．4，3．5)=1．092 5，代入经验公式中。在原尺寸下，仿真结果与等效电路模型结果的传输系数曲线如图3所示。在尺寸变化为p=24．8 mm，w1=0．2 mm，w2=7．0 mm，d=22．0 mm时，仿真结果与等效电路模型结果的传输系数曲线如图4所示。

3 结语
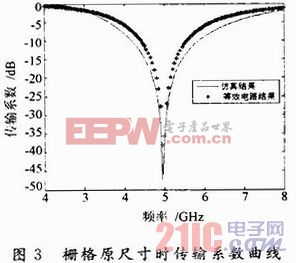
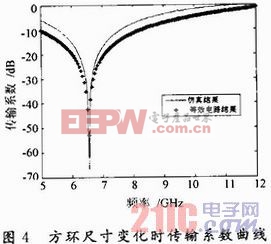
由图可知，仿真结果与等效电路模型结果吻合程度高，而且在一种尺寸下得到的等效介电常数表达式在尺寸变化不大的时候也仍然适用，从而说明通过此方法得到的εeff表达式比较精确，可以改进频率选择表面等效电路模型。