降压开关电源设计过程中控制技术分析及选择

降压开关电源的设计过程非常简单，从最初的规格说明出发，为设计选择合适的“核心电路”，再配置一些外部元件，最 后仿真和验证以完成设计方案。但是目前有很多种控制技术，如何做出合适的决定很具挑战性。为了选择更合适的控制器或调节器，必须进行深入的研究。

经典的PWM控制技术

最常见的控制器采用经典的脉冲宽度调制 (PWM) 技术，利用内部时钟引导每个工作周期的开始，使主MOSFET导通。通过比较控制电压 (Vc) 和锯齿波电压幅度(Vp)，能够对关闭时间进行定时，如图1所示。

图1 电压模式降压稳压器的基本架构

锯齿波有三种不同的生成方式，与之对应的是电压模式、电压型前馈控制和电流模式这三种控制技术。

电压模式：经典

控制器内部产生一个恒定的锯齿波，它具有恒定的电压幅度。

电压模式避免了电流模式斜率补偿所带来的复杂度增加，不容易受噪声影响，而且通常检测输出电流所需的消隐时间更短。环路增益和带宽也随着输入电压的增加而增大。

因为简单，电压模式广泛使用在低输出电流的应用中，此时输入线路相对稳定，具有比较慢的线路瞬态变化。

调制器和功率级的增益如下：

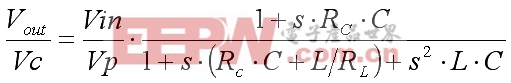
(1)
这里，Rc是输出电容的ESR，是输出负载的阻抗;L和C分别是输出滤波器的电感和电容值，调节器的环路增益H(s)表示成：

(2)

调制器和功率级的增益直接跟随输入电压(Vin)的增加而增加。和频率相关的项是LC网络的传输函数。该网络具有电感和输出电容所引入的双重极点，同时还具有一个零点，该零点由输出电容C和它的ESR造成。

电压型前馈控制

锯齿波的斜率随输入电压变化，而且消除了输入电压变化导致的环路增益和带宽的可变性。电压型前馈控制避免了公式(1)和(2)对输入电压的依赖。

线路瞬态响应也有所改善，这是由于调节器在输出电压发生变化之前(输入电压的变化所致)就改变了占空比。电压型前馈控制所带来的另一个好处在于可以在输入电压的整个变化范围内优化环路增益。

电流模式：传统而且高性能

电流模式并没有使用恒定的锯齿波来控制占空比，而是采用了输出电感电流所产生的锯齿波(见图2)。电流检测放大器通过测量主MOSFET导 通时的电流来检测电感电流。添加了固定的校正斜坡，从而消除了占空比大于50%所带来的次谐波振荡问题。在开关周期的开始阶段，开关打开，Rs和电流检测放大器检测电感电流。然后把电流检测信号加到校正斜坡中，当这两个波形的和超过Vc时，比较器的输出变低，关闭输出开关。在电流模式技术中，调制器、输出开关和电感的工作原理类似于跨导放大器，给输出提供一个经过调节的电流。结果，由于属于基本的电压模式控制，该级的增益不受Vin的变化影响。但是，该级的增益将随负载阻抗发生变化。

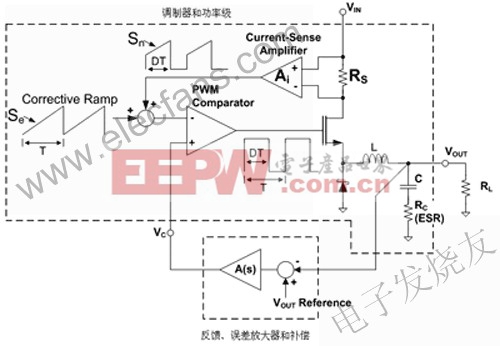
图2 电流模式降压稳压器的基本架构(LM5642)

电流模式控制具备以下一些优点，例如：并行连接的相位之间存在着更好的电流共享，L-C输出滤波器的单极点带来了较好的频率补偿，具有精确的逐周期电流限制以及对输入干扰不敏感等。

如果我们对传统电流模式控制器的补偿级进行深入研究，会发现调制器和功率级的增益如下：

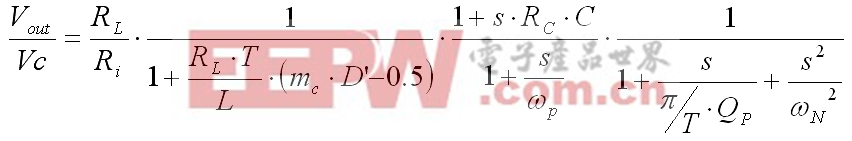
(3)

　　这里，Ri是电流检测增益:Ri=Ai·Rs (4)

　　D’是关工作周期:D’=1-D (5)

　　斜波补偿因子表示为:

(6)

　　其中，Se是校正斜坡的斜率， Sn是检测到的电流波形的斜率。

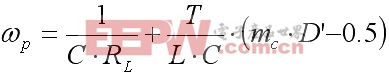
(7)

　　阻尼因子表示为：

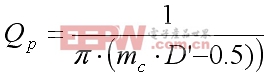
(8)

　　公式(3)中的第一项表明增益是负载阻抗RL和电流检测增益Ri的函数。第二项给出了斜波补偿项。当校正斜坡斜率Se大于电流波形的正斜率Sn时，斜波补偿因子Mc充分增加，从而对增益进行衰减。

　　第三项给出了起决定作用的低频特性。它具有一个由输出电容的ESR引入的零点，以及单极点wp，该极点的数值由输出电容和负载阻抗决定。

　　第四项包含两个位于开关频率一半处的极点。这些极点的峰值受阻尼因子Qp控制，而阻尼因子又进一步受校正斜坡控制。如果斜坡太小，这些极点将使调节器的环路增益到达最高点，如果占空比大于50%，在一半开关频率处的环路增益将超过0dB。这将导致电流模式控制发生次谐波振荡。

　　电流模式控制最主要的弱点在于，难以测量具有小占空比的电流。这种测量方式易受噪声影响，并且调制有时可能会不稳定。

　　磁滞控制技术：简单快速
另一个可能的方案是磁滞控制技术(见图3)。调制器就是一个具备内置输入磁滞(几毫伏)的比较器，用于比较反馈电压和参考电压。当反馈电压大于参考电压半个磁滞电压时，比较器的输出变低，关闭开关。开关将一直保持关闭状态，直到反馈电压跌到比参考电压低半个磁滞电压为止。

　　图3 磁滞降压稳压器的基本架构(LM3485)

这种拓扑结构可以对负载瞬态变化做