一种结构简单的低功耗振荡器电路设计

摘要：给出了一种结构简单的低功耗振荡器电路的设计方法，该电路由RC充放电回路、偏置电路组成。与传统振荡器电路相比，该电路具有精度高、电路结构简单以及输出占空比可调等优点。采用0．35 μm BCD工艺并利用Cadence Spectre仿真工具对电路进行仿真，结果表明，在5 V工作电压下，电路起振速度快，输出波形稳定，平均功耗仅0．29 mW。
关键词：振荡器电路；低功耗；RC振荡器；CMOS

0 引言
振荡器是许多电子系统中时钟产生电路的重要组成部分。常用的振荡器结构有RC振荡器、环形振荡器和晶体振荡器三种。RC振荡器结构简单，成本低，且电路功耗也较低，因而成为应用最普遍的一种振荡器电路；但它有振荡频率稳定性差，产生的频率受电源电压、环境温度以及组成振荡器的各种元器件的电学特性影响较大等缺点。
本文基于对传统RC振荡电路的分析，提出了一种新型的RC振荡电路。该电路结构简单，能够在不增加功耗的同时提高RC振荡器的精度，且温度系数小。此外，与传统RC振荡器相比，由于该电路包含两个充电支路，因此，电路输出波形的占空比可随意调节。

1 传统RC振荡器
图1所示为传统的RC振荡器电路，电路由保护电阻Rp、反馈电阻Rf两个反向器U1和U2，以及一个耦合电容C组成。当节点电压Vi有极微小的正跳变发生时，U1的输出迅速跳变为低电平，同时U2的输出迅速跳变为高电平，电路进入第一个暂稳态，此时电容C开始通过电阻Rf放电。随着电容C的放电电压Vi逐渐下降，当Vi下降到MOS管的阈值电压VTH时，U1反向器的输出迅速变为高电平，而U2反向器的输出迅速跳变为低电平，电路进入第二个暂稳态，电容C通过电阻Rf开始充电。随着电容C的充电，Vi不断升高，当Vi升至VTH时，电路又重新转换为第一个暂稳态。

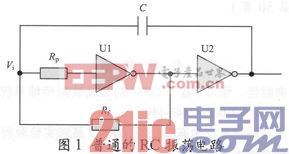
假设保护电阻Rp足够大，且Rf远大于反向器的导通电阻RON，则电路的振荡周期为：
T=2.2RfC (1)
图1中，RC振荡器的频率主要受电阻Rf、电容C以及反相器U1、U2的翻转电平影响。U1、U2的翻转电平受反相器内部器件的特性和电源电压的影响较大，并且该振荡器的频率精度不高，波形占空比不易调节。

2 新型振荡器设计及分析
本设计的新型振荡器电路结构如图2所示。图2中左边的电路上下对称，MOS管T5、T6以及反相器、与非门构成振荡器的主体部分，其余的器件为偏置部分。电容C1、C2的充放电时间决定着振荡频率，因此，通过改变C1、C2的电容值可以改变振荡器的输出频率。

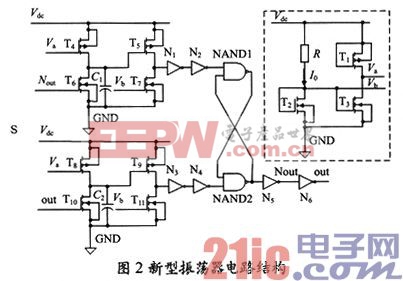
电流镜及电压偏置电路部分如图2中的虚框所示，其作用是为RC充放电支路提供偏置以及控制支路电容充电电流的大小。电流镜产生的基准电流(即流经电阻R的电流)的计算公式如下：

式中，Vb为T3、T7和T11三个NMOS管提供的栅极偏置电压。它通过电流镜结构来镜像R支路的电流。这样，就可以计算流过T3管的电流I1为：

式中，Si表示Ti管子的宽长比(以下公式皆如此表示)。
图2中，Va为T4和T8两个PMOS管提供的栅极电压偏置，电压为：
Va=Vdc-|Vtp|
振荡器的输出频率主要由环路延迟时间来决定，而电路中反相器和RS触发器等的延迟时间比较小，因此，延迟时间主要由电容C1、C2和给电容充电的电流、MOS管T5的开启电压决定。
下面主要分析电容C1充电而电容C2放电(即Nout处于低电平，out处于高电平)时的过程。如图2所示，电容C1充电电流的大小由I0决定，电容C2放电电流则由T10管栅极电势out及T5管栅极电势决定。当Nout为低电平时，T6管关断；同时out为高电平，T10管开启；Vdc通过PMOS管T4给C1充电，其充电电流为：

由图2所示的电路结构可知：当Nout为高电平时，T6管强反型导通，电容C1放电，最终使电容C1两端的电压差为0。此时，电容正端电压VC为最低，式(5)中的VC(t)=0。由此可以得知，电容C1的充电时间为：

另外，由图2电路可知，C1被充电直到T5管关断为止，此时T5管漏极输出为低电平，并通过环路将Nout置为高电平，T6管开启，C1充电结束，开始放电。因此，VC的最高电压为使T5管关断时的栅极电压。当T5管的|Vgs|小于其阈值电压|Vtp|时，T5管关断。假设|Vgs|=|Vtp|时的T5栅极电压为VC的最大电压，即：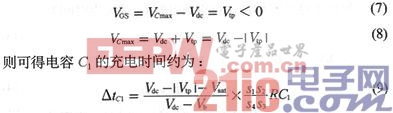

C2通过T10放电将拉低C2正端电位。由于out为反相器输出，所以out的高电平约为Vdc；而C2正端电位最高也比Vdc低一个|Vgs9|，所以，NMOS管T10在导通的过程中有VC2≤Vgs10-VTN，器件工作在线性区。这样，T10的导通时电流为：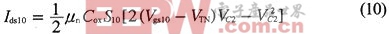

式中，Vgs10=Vdc；VC2为电容C2的正端电压。这样，根据式(10)就可以计算出T10管在线性区导通电阻的平均值RON。电容C2通过T10管放电至0处，其放电时间常数为：
τC2=RONC2 (11)
由于图2中的两个充放电支路是对称的且对应器件的参数一致，电容C1、C2的充电与放电时间仅由其电容值决定。当C1、C2在同一个数量级时，我们可以得到两个电容的充电时间远大于其放电时间，振荡器的周期由两个电容的充电时间共同决定。△t≥T是图2所示振荡器起振的充分条件，当△tT时，振荡器不能正常工作。
当C1上极板的电压上升到最大值Vdc-|Vtp|时，T5管瞬时关断，维持短暂的环路延时时间后，Nout变为高电平，C1开始放电，同时out变为低电平，C2开始充电。在T5管关断期间，其漏极变为低电平，通过两个反向器反相后，与非门NAND1与N2相连的输入端为低电平，NAND1输出为高电平。图2中的两个电容充电支路参数完全相同，且Nout和out信号互补，即当Nout为高电平时，out为低电平，反之亦然，可得当N2输出为低电平时，N4输出为高电平。NAND2输出被锁定在低电平，直到电容C2的上极板被充电到最大电压值Vdc-|Vtp|，NAND2翻转为高电平。即：当电容C1电压从0充电到Vdc-|Vtp|这段时间里，振荡器输出为低电平，而当电容C2电压从0充电到Vdc-|Vtp|这段时间里，振荡器输出为高电平。
整个电路的反向器和RS触发器的延迟时间比较小，因此在理论计算时可以忽略。振荡器输出端out的高电平由电容C1的充电时间决定，而低电平由电容C2的充电时间决定。在电路结构对称的情况下，改变电容C1、C2的比值，就可以改变振荡器输出波形的占空比，其占空比为：。
本电路的设计电压Vdc为5 V，将各个参数代入公式可得：
△t1=12．223RC1 (12)
根据电路的对称性，可得到电容C2的充电时间为：
△t2=12．223RC2 (13)
振荡器的周期为：
T=△t1+△t2 (14)
若选取C1=C2=769．356 fF，R=481．763 kΩ，则振荡器的周期为：
T=2△t1=2×12．223×481．763×103×0．769356×10-12=9．06μs

3 结果分析
基于0．35 μm BCD工艺，并采用Cadence Spectre仿真工具对图2所示电路进行仿真的振荡器电路输出电压波形如图3所示。通过图3可以看出，振荡器的起振时间非常短，在一个周期内就能有稳定的输出；振荡周期为10．02 μs，而理论计算值为9．06 μs。理论值与之相比偏小的主要原因有两个：一是计算过程中忽略了环路中的反相器和RS触发器等的延迟时间以及电容的充电时间；二是在电容充电过程中，充电电流并不是恒定值。