基于Multisim10和Matlab7．0的正弦稳态电路分析

摘要 使用计算机仿真软件可以方便地帮助学生完成虚拟实验过程和复杂的数学计算。文中提供一种将仿真软件Multisim10和Matlab7．0结合使用分析电路方法，以分析计算RLC串联正弦稳态电路为例，仿真的过程和结果充分发挥了Multisim和Matlab软件的作用，并互相弥补不足。此方法的引入有助于学生对电路分析基本方法的理解和掌握。
关键词 Multisim10；Matlab7．0；正弦稳态电路；电路分析基础

Multisim是一款专门用于电子线路仿真和设计的EDA工具软件，其提供了一个虚拟的电子实验工作台，以其界面友好、功能强大和易用性受到电子类专业人员的青睐。Matlab是一款商业数学软件，Matlab编程语言简单易用，软件具有强大的数据处理能力，可用于算法开发、数据可视化、数据分析以及数值计算等。
电子类课程教学过程中，由于教学资源的限制，并不能实际演示电路实验，此时使用Multisim可以仿真实验过程，用Matlab可以精确地完成电路计算。实际上，使用Multisim可以得到直观的电路图形界面并体现实验的操作方法，但往往不能全面显示计算结果，也无法体现分析方法；Matlab则以数值计算、图形绘制见长，其编程过程反映了分析方法，但无法体现直观的电路图形。文中将两款软件综合使用，以仿真分析正弦稳态电路为例，将二者优势结合，全面反映电路的分析和实验过程。

1 正弦稳态电路及其分析方法
在正弦激励的动态电路中，若各电压、电流均为与激励同频率的正弦波，则该电路即为正弦稳态电路。正弦稳态分析主要包括求解其稳态响应，计算功率以及最大功率传输定理等。分析正弦稳态电路，往往采用相量分析的方法，画出电路图的等效相量模型，然后按照分析直流纯电阻电路的方法进行分析计算，得到复数域下的节点电压和支路电流，再将其转化为时域下的结果。

针对于电路负载的功率，当负载电阻及电抗均可独立变化时，根据最大功率传递定律，当负载的阻抗ZL与电路的输出阻抗ZO满足共轭匹配时，负载所得到的功率最大。由此可见，当电路较为复杂时，上述过程的手工计算量较大。使用仿真软件可以实时、动态地得到实验数据和计算结果。

2 正弦稳态电路的仿真与分析
下面以一道具体的正弦稳态电路分析问题为例，阐释Multisim仿真和Matlab仿真在电路分析上的长处和不足，并引出综合使用的方法。
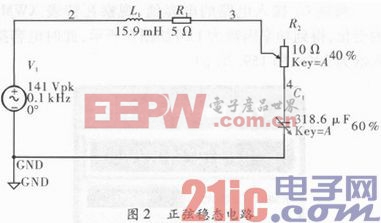
RLC正弦稳态电路如图2所示，其中V1为电压源；峰值141 V；频率100 Hz初相为0；电感L1值为15．90 mH；R1大小为5 Ω，可变电阻R2(变化范围0～10 Ω)；C1为可变电感，变化范围0～318．60μF。

(1)当R2=4 Ω，C1=191．60μF时，R2两端电压、C1两端电压、电源电压三者的幅值和相位关系，求解此时电源提供的复功率和功率因数。
(2)R2=4 Ω，则C1为何值时，电路的功率因数最大。
(3)当电阻R2和C1的参数都任意变化时，研究负载的功率变化并求负载的最大功率。
(1)基于Multisim10的仿真分析。在Multisim的Workspace中搭建图3所示的电路，为解决问题(1)，调整R2和C1的接入值，使R2=4 Ω，C1=191．60μF。其中瓦特表XWM1用来显示电源输出的有功功率及功率因数，瓦特表XWM2用来显示负载的有功功率及功率因数，示波器XSC1用栗显示负载R2和C1两端电压波形。

如图4所示，瓦特表XWM1显示值为问题(1)中电源提供的有功功率和功率因数，图5为此时R2和C1两端的电压波形。可以读出此时电路有功功率约为1．07 kW，功率因数约为0.98。示波器可以大致读出R2和C1两端电压的峰值，但不能得精确的相位差。
调整C1接入电路的电容值，观察瓦特表XWM1的变化，得到功率因数为1时如图6所示，此时电容接入恰为50％，即159．30μF。

调整R2接入电路的阻值和C1接入电路的电容，观察瓦特表XWM2的示数到最大，电容C1和电阻R2值，此时C1和R2各接入50％。C1=159．30 μF，R2=5Ω。XWM2的示数如图7所示。

可见Multisim为用户提供了交互式的仿真环境，但不能得到R2和C1端电压的波形函数，以及电压相位差；在调节R2和C1的过程中，其接入值也并非连续变化，而是以每次最小变化的离散值进行调整的，在解决(2)、(3)问题时，找R2、C1参数的过程繁琐，而且不能确定最终的接入值是精确的。使用Matlab进行编程，可以克服这些问题。
(2)基于Matlab7．0的仿真分析。根据正弦稳态电路的分析方法设计算法，编写Matlab程序代码，计算并显示结果。先将电路给出的各个参数表示成复数域下的形势，对于问题(1)，求解出R2和C1上的电压相量后，用abs函数和anglg函数分别显示出电源电压、R2和C1上电压的幅值和初相角，并调用compass函数绘制出这3个电压量的极坐标图；问题(2)则应用电路功率因数为1时，电路呈现纯电阻电路的特点，解出C1的值；对于问题(3)，不直接采用最大功率传输定律的方法，而是运用数学解析方法，将负载的功率P表示成C1和R2的函数，调用Matlab的diff函数和solve函数，求解方程组

找到P的极大值以及此时对应的C1和R2，解析法的求解结果可与应用最大功率传输定律所得结果进行比对，验证该定律的正确性。为直观看出C1和R2变化时功率P的变化情况，将C1和R2用向量矩阵表示如其变化范围、精度后，调用mesh函数，绘制出以C1和R2为自变量时因变量P的三维图像。
程序运行后，显示了所求结果的精确值。对于问题(1)，根据UR2和UC1的幅值、相位的具体值可以得到其具体的波形函数UR2=61．60cos(200πt／s-0．06π)，UC1=127．92cos(200πt／s-0.56π)，UR2超前UC1π／2，图8给出了Us、UR2、UC1在极坐标系下的幅值相位关系图。此时的电路功率因数λ～0．98，有功功率P=1．07×103W，无功功率Q=199．63 W；问题(2)可得到电路功率因数λ=1时，C1=159．31 μF；图10为R2和C1参数改变时，负载功率P变化的三维图像，峰值处对应图对应P最大时的C1和R2的参数，此时C1=159．31μF，R2=5 Ω。带入后验证ZC1+ ZLt=0，R2=R1成立。解析结果证明了最大功率传递定理。