电机逆变器死区补偿独领风骚高性能伺服不在话下

现今工业伺服驱动中多采用驱动永磁同步电动机(pmsm)的交流伺服系统，其交流驱动单元使用三相全桥电压型逆变器。pwm调制的变频控制技术实现了对交流电机动态转矩的实时控制，大大提高了伺服系统的控制性能。然而，对于pwm逆变器，在驱动功率管的开关信号中插入延时时间以防止直流母线直接短路，延时时间的引入将导致死区时间效应，引起逆变器输出波形的畸变和基波电压的降落，影响了伺服系统性能的进一步提高。

逆变器死区补偿方法综述

为补偿td引起的电压波动，研究人员提出了各种补偿方法，大致可划分为三类。

最普遍的方法是在电流极性相同的区间内，根据缺少的脉冲列相应加上极性相反的脉冲列，以抵消其影响。由于三相电流必有一相与另两相极性相反，一种简单的方法是对极性相反的相实行二倍的电压过补偿，使三相电压死区影响相互抵消，线电压波形为正弦形。文献详细分析了死区产生的原因和影响，并根据模拟调制和数字调制分别给出了死区的硬件电路补偿方法。根据全桥电路的开关状态，提出了一种带死区补偿的逆变器数学模型，该模型的特点是由简单的滞环结构组成，根据此模型可由一计算公式实现死区补偿。

第二类方法是根据无效器件原理实现死区补偿的。在任意时刻，逆变器每一桥臂两个功率器件中只有一个是有效的。当上桥臂器件关断时，不论下桥臂器件是否导通，输出电压都是直流母线的负端电压，此时称下桥臂器件是“无效”的。死区补偿的办法是，维持有效器件的驱动信号不变，改变无效器件的驱动信号使之满足设置死区的要求。既然“无效”器件的通、断并不影响输出电压状态，那么也就不需要驱动信号了，只给有效器件发出驱动信号就可以了，这样也就不需要加入死区，也就没有什么死区补偿的问题了。但该方法在电流过零点处会由于误差导致畸变，因此使用这个方法时要注意电流过零区域的处理。一些学者进一步提出了改进方法。在电流过零点加一滞环，在滞环时间内使用正常的开关死区保护，可减小畸变。由于电流采样中的干扰和电流变化的复杂性，在电流过零点附近的区域应给出两路驱动信号并加入死区及死区补偿。利用pwm关断时刻实现换流时的开关死区保护，可消除开关死区的影响。

第三类方法是电流预测控制。建立较为准确的电机系统模型，分析电流波形的畸变量，通过电流的预测控制来实现电流波形的校正。预测电流控制的死区问题，通过估计反电势补偿电压波形畸变和电流零点钳位现象。建立异步电机模型的矩阵方程，根据对svpwm算法里定子相电流的预测，补偿其空间电压矢量。利用d-q旋转坐标系下的pmsm模型设计观测器，观测q轴损失的电压，通过公式折算成需补偿的死区时间tc，实现死区的在线补偿。时间延迟控制来估计死区导致的干扰电压，并将其反馈到电压参考给定上以补偿死区影响。电流预测方法计算繁琐，且补偿效果与电机模型的精度和时变的参数值直接相关，不易得到满意的效果。 逆变器死区的影响

由pwm死区时间产生的基本原理可知，引起的逆变器输出电压的偏差脉冲在绕组电流周期t1内的电压偏差可用一方波来等效，为了分析方便，假定电压偏差脉冲在时间上是等间距的，则等效方波的高度为：

随着电流极性的变化，误差电压脉冲的方向也随着发生变化，而且随着载波频率的提高，误差电压脉冲出现的次数也随之提高，虽然死区时间很短，只有几个微秒，但是误差电压在一个周期之内累积起来，也会对输出电压的基波幅值产生较大的影响。误差电压与理想电压、实际输出电压的定性关系如图2所示。

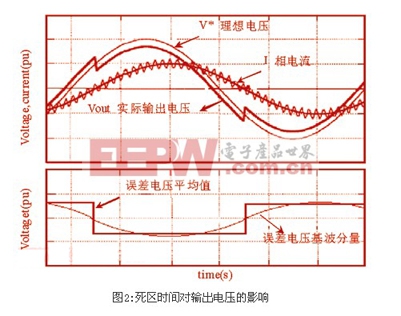
对图2中的偏差方波进行傅立叶分析得到：

其中，ω1电流基波角频率;ψ期望电压与电机电流之间的相位差。

因此，在忽略功率开关引起的高频噪声的情况下，逆变器的输出电压为：

其中，ma调制度，为调制正弦波幅值与三角波载波幅值的比值。

由上式可知，由于逆变器死区时间的存在，不但使逆变器输出电压的基波发生变化，而且使输出电压中含有3次、5次、7次等高次谐波。

开关死区造成逆变器输出电压波形发生畸变，导致输出电流波形波形畸变，即电流的交越失真。

·死区时间越长，逆变器输出基波电压损失越大，电压波形畸变程度越大;负载基波电流幅值下降越多，电流波形畸变也越严重。

·对于确定的死区时间，负载功率因数变小时，会使逆变器输出基波电压幅值增加，电压波形畸变率变小，基波电流幅值减小，电流波形畸变率变大。

·当输出电压较低时，空间电压矢量幅值很小，三路桥臂相对导通时间变短，死区时间的影响变大。

·死区不仅影响输出电压幅值，还影响其相位;死区使pwm波形不再对称于中心