基于特征选择改进LR-Bagging算法的电力欠费风险居民客户预测

对欠费比例的一种影响。若WEO_i表示离散变量的第i个类值的证据权重，则有：

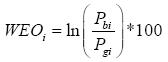(8)

其中，P_bi和P_gi分别表示离散变量取第i个类值时，欠费风险客户占比和非欠费风险客户的占比。

最后，随机抽取已完成前述处理的居民客户样本的10%，共条记录作为构建模型的初始数据 。

3.3 建模

3.3.1 本文改进算法模型

基于特征选择改进的LR-Bagging组合模型虽然增加了分类结果的精度，但特征选择的随机性也不可避免的增加了模型的偶然性。显然，每一次特征变量个数发生改变。在其他条件不变的状态下，随着循环次数的增加，至于特征变量的个数对模型结果的影响规律，我们甚至无法预知。对此，本处采用了实证比较的方法来初步确定上述两影响因素的最优数值，即通过不断改变特征变量探究模型效果的变化。模型的效果的好坏仍采用采用AUC值来衡量。即令特征变量个数k满足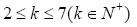：，同时，基于经验，我们设置训练集与测试集的样本比例为7：3，ε的值为0.05，则利用本文算法可以得到不同的组合模型。

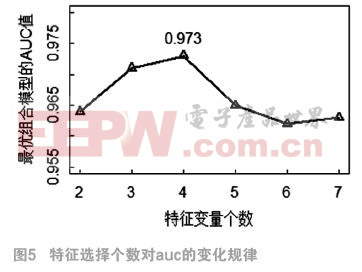
观察图5不难发现，在其他条件不变的情况下，随着特征变量个数的增加，AUC总体呈现先增长后下降的的变化趋势，且当k取值为4时，AUC最大，因此大致可以认为4为其最佳特征个数，选取 时的组合模型为本文改进算法得到的最终模型。

3.3.2 单一逐步逻辑回归模型

对初始数据S通过逐步筛选建立逻辑回归模型，结果为：

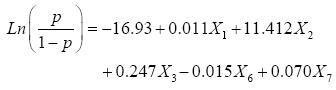
各系数均通过了0.05显著性水平下的公式(6)的正态分布检验。因此，该模型是显著有效的。

4 模型评估

分别采用本文基于特征选择改进的LR-Bagging算法的组合模型与单一LR模型对全量居民客户的风险概率预测，并借助预测结果对两者的准确性与有效性做出评估。

4.1 准确性—ROC曲线

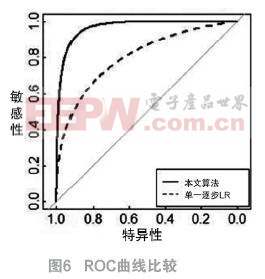
图6表明，基于本文算法模型的预测电力欠费风险客户的ROC曲线一直位于单一LR模型预测结果的ROC曲线上方，因此，可以认为，前者的准确性优于后者。

4.2 有效性—提升度

提升度(Lift)是评估一个预测模型是否有效的一个度量。这个比值由运用和不运用这个模型所得来的结果计算而来。一般来说提升度越大，效果明显。

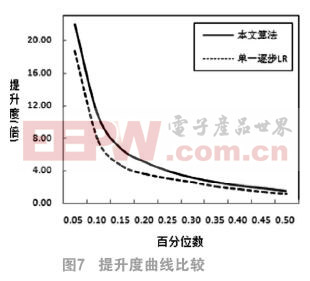
图7表明，基于本文算法模型的预测电力欠费风险客户的提升度曲线一直位于单一LR模型预测结果的提升度曲线上方，因此，可以认为，前者的提升度较大，有效性优于后者。

5 结论

本文从电力欠费风险预测的角度出发，提出了一种基于特征选择改进的LR-Bagging(即以逻辑回归为基分类器的Bagging集成学习)算法，其精髓在于每一个训练的LR基分类器的记录和字段均通过随机抽样得到。且算法的终止迭代准则由AUC统计量的变化率决定。该改进算法充分考虑了LR的强泛化能力、bagging的高精确度以及特征选择带来的LR基分类器的多样性、弱化的多重共线性与“过拟合”度，效果优于单一LR模型。且最终的实验表明，该改进算法得到的电力欠费居民客户风险预测模型的准确定性与有效性得到提升。而下一步，可针对改进算法中最优变量个数的确定问题展开探讨，或考虑将其推广至其他应用领域。

参考文献：

[1]顾曦华.济南供电公司电力大客户欠费风险预警研究[D].保定:华北电力大学,2007.

[2]田慧欣,王安娜.基于增量学习思想的改进AdaBoost建模方法[J].控制与决策,2012,27(9):1433-1436.

[3]李亚林,王茜.对电力营销中全过程电费风险管理的探究[J].电力技术,2016,1(148):165-165.

[4]张宇献,李松,董晓.基于特征聚类数据划分的多神经网络模型[J].信息与控制,2013,42(6):693-699.

[5]朱志华.电力客户信用评价与欠费风险预警系统的总体设计[J].现代计算机(专业版).2009(01):188-190.

[6]周晖等.基于Logistic回归模型的电力客户欠费违约概率的预测[J]. 电网技术,2007,31(17):85-88.

[7]黄文思.基于决策树算法的电力客户欠费风险预测[J].电力信息与通信技术,2016,14(3):20-22.

[8]马新宇.基于Bagging集成学习的水华预测方法研究[J].计算机应用化学,2014,31(2):140-144.

[9]Ma Ranran. Research of Ensemble Learning Algorithm. Shandong:Shandong Univerity of Science and Technology,2010.

[10]朱绍文,胡宏银,王泉德,等.决策树采掘技术及发展趋势[J].计算机工程,2000,26(10):1-3.

[11]李海波,柴天佑,岳恒.浮选工艺指标KPCA-ELM软测量模型及应用[J].化工学报,2012,63(9):2892-2898.

[12]马冉冉.集成学习算法研究[D].济南:山东科技大学,2010.

[13]施彦.物流中心选址的神经网络集成模型研究[J].计算机工程,2009,45(16):211-214.

[14]刘淑莲,王真,赵建卫.基于因子分析的上市公司信用评级应用研究[J].财经问题研究,2008,15(7):53-60.

[15]张克盡,陆开宏,朱津永,等.基于神经网络的藻类水华预