基于特征选择改进LR-Bagging算法的电力欠费风险居民客户预测

。

当然，LR作为回归模型的特殊形式，也需要满足经典回归模型的基本假设，违背这些假设显然会影响模型的分类效果，多重共线问题就是目前面临较多的问题。同时，逻辑回归的性能受特征空间的影响很大，也不能很好地处理大量多类特征或变量，这便是LR分类器的缺点所在。

2 Bagging集成学习

2.1 集成学习

集成学习^[8]是一种机器学习范式，它的基本思想是把多个学习器(通常是同质的)集成起来，使用多个模型(解决方案)来解决同一个问题。因其个体学习器的高精度和个误差均分布于不同的输入空间，从而能达到显著地提高学习系统的泛化能力的效果。

Breiman同时指出，要使得Bagging有效，基本学习器的学习算法必须是不稳定的，也就是说对训练数据敏感，且基本分类器的学习算法对训练数据越敏感，Bagging的效果越好。另外由于Bagging算法本身的特点，使得Bagging算法非常适合用来并行训练多个基本分类器，这也是Bagging算法的一大优势^[8]。

2.3 本文算法描述

前文指出，一方面，学习器的稳定性，即对训练数据的敏感性，很大程度上影响Bagging算法的效果，其中原因在于差异性小的数据对稳定性较强的学习器无法很好产生作用，这将影响到基学习模型的多样性，Bagging算法提高精确度的能力也将大大减弱，而LR模型的不稳定性能不突出;另一方面，LR对大特征空间的解释效果并不理想，且越多的变量特征也将加大变量间多重共线的可能性，LR模型的显著性无法得到保障。

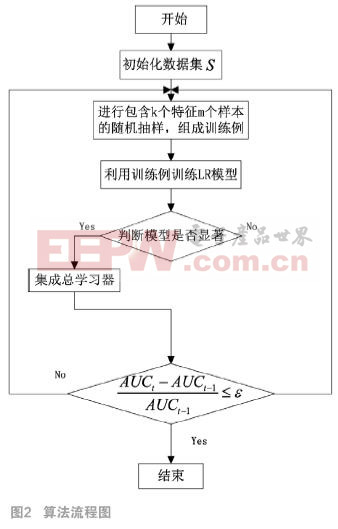
由于上述两点原因，本文提出了一种基于特征选择的LR-Bagging(基分类器为LR的Bagging算法)的改进算法。该算法的精髓在于对每一个LR进行训练的特征变量需要经过有放回的随机抽样产生。如此改进的目的在于通过减少或改变变量提高基LR分类器的多样性，减少变量间的多重共线性与过拟合问题，同时还能较好保留LR与Bagging集成学习的优点。

AUC(Area Under Curve)被定义为ROC曲线下的面积，它的取值范围介于0.5到1之间，是比较分类器间分类效果优劣的评价标准。AUC越大，我们认为模型的分类效果越好。一般情况下，，随着循环次数的增加，模型提取的数据信息量也会不断增加，最后达到峰值，所以我们通常可以认为组合模型的效果趋于先不断加强后保持稳定的过程。因此，我们把迭代的停止条件的设置为是合理的。

3 应用与结果

本应用以“电费回收风险”为主题，要求根据2015年8月至2015年9月贵州贵阳电网欠费居民样本客户的行为分析和特征拟合，以及与全量居民客户的特征匹配，采用分群管理理论和数据挖掘算法建立数学模型，计算出全量居民客户的电费回收风险程度，自动分析识别出欠费高风险居民客户群。

本部分主要通过改进的LR-Bagging算法与单一逐步逻辑回归算法在电力欠费高风险居民客户的预测的应用效果的比较来展开。借助的分析工具为R语言。

3.1 基于本文改进算法的模型流程图

针对本应用的实际情况，结合改进算法的数据需求，整体实际操作过程的流程可以表述如图3。

3.2 模型与结果

综上所述，有如下处理过程：

3.2.1 定义风险客户样本

业务经验告诉我们，并非所有的欠费居民客户都是存在欠费风险的客户，因为我们并不排除多数欠费居民客户因为忘记缴费日期而出现欠费的可能性。一般情况下，存在欠费风险的居民客户占全量客户的比例不超过25%。因此，考虑通过所有欠费居民客户在2015年8月至9月的累计欠费金额的四分之三分位点作为定义欠费风险居民客户的标准。

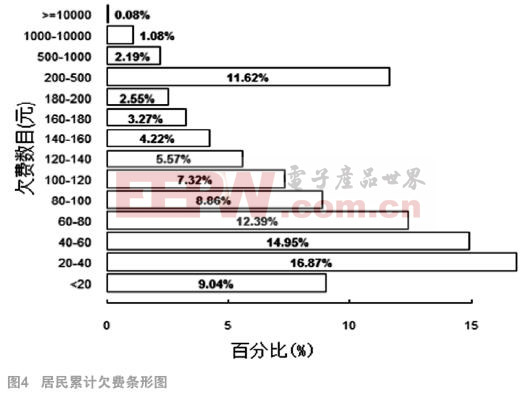
图4为全部居民客户在2015年8月至9月累计欠费金额的概率直方图，可以发现，大约75%的居民客户的累计欠费金额在140元以下。经过与电网专家的商讨，认为可选定该数据为是否为欠费风险客户的阈值。

综上所述，我们定义“坏客户”样本，即欠费风险客户样本的标准为：在2015年8月至9月期内，累计欠费金额超过140元的居民客户。

3.2.2 变量的构造与筛选

原始居民客户数据包含包括年龄、用电性质、合同容量等基本属性以及总用电量、电费实际金额等历史行为属性在内的25个字段，显然，变量个数过多，需要进行筛选，具体操作为：

对于连续型变量，计算其与因变量“是否为坏客户”的spearman相关系数，大于0.5的情况下保留;对于离散型变量，对其与因变量做卡方检验，保留在0.05显著性水平下的显著变量，最终确定的用于建模的变量为：平均用电量、平均电费、平均缴费时长、信誉分数、用电类别、行业代码、合同容量、城乡标志，对应地设置为X₁~X₈。

同时，考虑到离散变量对于逻辑回归的效果影响，基于目标变量对WEO其做编码处理。WEO叫做证据权重(Weight of Evidence)，表示的其实是自变量取某个值的时候