详谈Turbo码特点及应用分析

据排列顺序，避免置换前相距较近的数据在置换后仍然相距较近，特别是要避免相邻的数据在置换后仍然相邻。

Turbo码　　2) 尽量提高最小码重码字的重量和减小低码重码字的数量。

3) 尽可能避免与同一信息位直接相关的两个分量编码器中的校验位均被删除;

4) 对于不归零的编码器，交织器设计时要避兔出现尾效应 图案。

在设计交织器时，应考虑具体应用系统的数据的大小，使交织深度在满足时延要求的前提下，与数据大小一致，或是数据帧长度的整数倍。

交织器和分量码的结合可以确保Turbo码编码输出码字都具有较高的汉明重量。在Turbo编码器中交织器的作用是将信息序列中的比特顺序重置。当信息序列经过第一个分量编码器后输出的码字重量较低时，交织器可以使交织后的信息序列经过第二个分量编码器编码后以很大的概率输出较高重码字，从而提高码字的汉明重量：同时好的交织器还可以奇效地降低校验序列间的相关性。因此，交织器设计的好坏在很大程度上影响着Turbo码的性能。

交织器的类型可以分为两大类，一是规则交织器，也称确定性交织器，其交织器的映射函数可以由一个确定的解析函数给出。二是随机交织器，其映射函数不能由-个确定的解析表达式给出。

Turbo 码常用的交织器包括以下几种：分组交织器、随机交织器、s-随机交织器等等。

3. 删余技术

对于数字通信领域日益紧张的带宽资源，提高码率就意味着节省带宽和降低通信费用。删余(Puncturing)是目前提高Turbo码码率的主要方法。

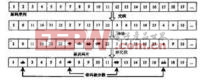
Turbo 码中，删余器通常比较简单，因为在一般的应用中，码率都是在1/2 或者1/3 ，因此即使有删余器，它一般也只是周期性的从两个分量编码器中选择校验比特输出即可。其具体做法是：从两个RSC编码生成的校验序列中周期地删除一些校验位，然后再与未编码的信息序列复用重组成最后的编码输出序列，调制后进入信道传输。若信息序列为d1 =(C11) ，长度为N ，那么两个RSC分量编码器的输出为：

Turbo码　　图3. 6 所示示为采用了删余技术的编码结构，若取RSC1输出的奇比特和RSC2的偶比特，即采用删余矩阵P= [ 10,01] ， 那么编码输出长度为2N，码率提高为1/2的序列为Cp.

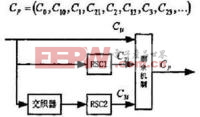
Turbo码　　两个分量码编码器的输出经过删余得到的序列被称为奇偶序列，是校验序列。一个好的删余算法应该符合以下几点要求：

1) 不能删除信息位.删除信息位会造成较大的信息损失，从而使误码率有较大的损失;

2) 删余应该在时间域上均匀进行，删余同一时刻所有的比特位会造成此时刻信息损失较大，影响误码率;

3) 删余应该对于各分量码均匀进行，从而使信息的损失均匀分布在各分量码上，避免由于信息损失不均匀导致分量码译码性能下降。

译码原理

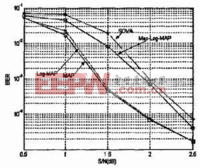
香农信息论告诉我们，最优的译码算法是概率译码算法，也就是最大后验概率算法(MAP)。但在Turbo码出现之前，信道编码使用的概率译码算法是最大似然算法(ML)。ML算法是MAP算法的简化，即假设信源符号等概率出现，因此是次优的译码算法。Turbo码的译码算法采用了MAP算法，在译码的结构上又做了改进，再次引入反馈的概念，取得了性能和复杂度之间的折衷。同时，Turbo 码的译码采用的是法代译码，这与经典的代数译码是完全不同的。

Turbo 码的译码算法是最早在BCJR 算法的基础上改进的，我们称以MAP算法，后来又形成Log-MAP算法、Max-Log-MAP以及软输入软输出(SOVA)算法。

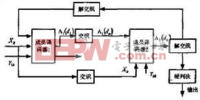
Turbo码　　Turbo 码的译码结构图

1.Turbo 码的译码结构如图所示. Turbo 译码器有以下的特点：

1) 串行级联

2) 迭代译码

3) 在迭代译码过程中交换的是外部信息

2. 概率译码译码原理及结构

译码时首先对接收信息进行处理，两个成员译码器之间外部信息的传递就形成了一个循环迭代的结构。由于外部信息的作用，一定信噪比下的误比特率将随着循环次数的增加而降低。但同时外部信息与接受序列间的相关性也随着译码次数的增加而逐渐增加，外部信息所提供的纠错能力也随之减弱，在一定的循环次数之后，译码性能将不再提高。

译码算法

如前所述，turbo码需要一种软输入软输出的译码算法。软输出译码器的输出不仅应包含硬判决值，而且包括做出这种判断的可信程度。

Turbo码　　译码算法应该考虑到三方面的问题，及外信息的引入;如何在迭代译码中充分利用各类信息，防止简单正反馈的形成，确保算法收敛;充分利用码原件的相关信息。常见的算法有一下几种：

1. 标准MAP算法

是对bahl软输出算法做一定修正后，通过除以先验分布来消除正反馈的算法。对于约束长度为M 1的卷积码，其运算量为每比特6x3^M次乘法和5x2^M次加法。由于乘法运算量大，限制了译码的规模和速度。

2. Log-MAP算