一种EKF改进算法探讨

根据第1节中建立的系统模型，系统测量值yt为2参数，系统状态参量xt为8参数，为了得到准确解，故而需要至少4颗有效卫星的测量值。为了能够满足用户需求的定位精度，本文提出利用一般车辆行人等用户在垂直地面方向上的位置变化缓慢这一运动特性，增加如下方程：

式(17)中，R1为从用户在ECEF坐标系下的状态参量xt到用户在NED坐标系下的状态参量mt的转换矩阵，利用坐标系旋转的原理可以求得。A2为用户在NED坐标系下的状态参量mt的一步转移矩阵。它们的表达式如下：

综上所述，得到改进的EKF算法的计算过程如下：

根据理论分析可以得出，改进的EKF相对于普通的EKF来说，增加了一项先验信息，故而使得只有3颗有效卫星时的定位解算有了4个解算方程，因此可以相对准确地解算出4个未知数的值;而在有效卫星数不少于4颗时，增加的方程(15)仍然满足，故而也不会影响定位精度。

3 算法仿真和分析

在本文的算法验证实验中，使用了Leika GPS1200测量型接收机在车载动态下采集的GPS信号的伪距和伪距增量的测量值，其中伪距测量值经过伪距增量测量值的平滑。算法的验证是在PC机上使用Matlab完成的。

在算法验证中，设置采样时间间隔为T=1 s。接收机的运动状态为从静止状态变化到在地面上高速运动最后又逐步静止。测试数据长度为2 500 s。参考轨迹是接收机使用动态实时差分(RTK)方法测定的，方差精确至毫米级。分别在有效卫星不少于4颗和只有3颗的情况下，比较了几种定位解算算法的定位结果。3.1 有效卫星数不少于4颗时的定位结果

以有效卫星数为4颗为例，分别使用ILS、EKF和改进的EKF算法进行定位，得到以ECEF坐标系下XYZ三维坐标表示的定位结果，如图1所示。

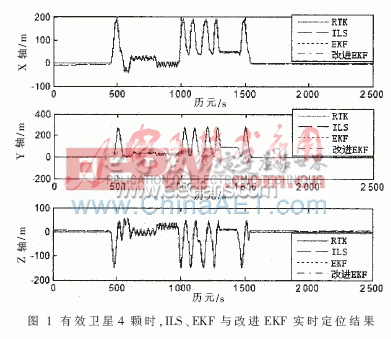
由图 1可知，接收机在前400 s时基本保持静止，然后开始运动至1 600 s，最后逐步静止至测试结束。三种解算方法都可以较好地进行定位解算。为了更好地分析定位结果，画出图 1中的XYZ三维坐标上的定位误差的均方根，如图 2所示。

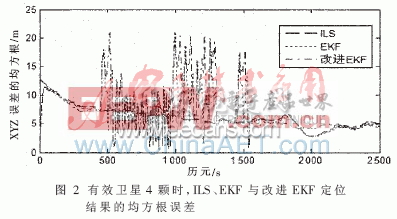
为了更好地比较ILS、普通EKF与改进EKF算法，计算图 2中三种算法在XYZ三个坐标方向上的定位结果的均方根误差的平均值，如表1所示。

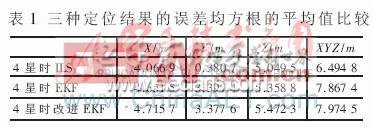
从图2和表1可以更清晰地看出，在有效卫星不少于4颗时，三种算法在以ECEF坐标系表示的XYZ方向上的定位误差的均方根均不超过20 m，平均定位误差不超过10 m，定位解算精度都很好。其中改进的EKF与普通EKF定位精度相当，而ILS的定位均方根误差抖动很小。这是因为，每当有新的测量数据时，ILS算法都会经过多次迭代计算直至结果收敛，而EKF与改进的EKF算法均只是利用新息进行一次计算，计算量要远远小于ILS，故而定位结果会稍有抖动。

3.2 有效卫星数只有3颗时的定位结果

在有效卫星数只有3颗时，ILS无法进行定位。分别使用普通EKF和改进的EKF算法进行定位，得到在ECEF坐标系下的XYZ三维坐标上的定位结果，如图 3所示。

为了更好地分析定位结果，画出图 3中的XYZ三维坐标上的定位误差的均方根，如图 4所示。

为了更好地比较普通EKF算法