无芯射频标签散射场分析和极点提取研究

摘要：目标雷达散射截面(RCS)，在复平面可以表示为复频域的函数。根据奇点(SEM)展开(留数)方法，计算对目标物体的散射奇点(留数)，进行射频识别(RFID)，是射频识别的新思路。通过FEKO软件，对蝶形无芯标签结构进行仿真得出该结构散射场。仿真的结果显示该结构具有开槽数量多、极点分布规律、数据容量大、易于实现等优点。
关键词：雷达散射截面(RCS)；奇点展开法(SEM)；散射场；FEKO

0 引言
射频识别是一种全自动，非接触识别方式。射频识别的系统就是阅读器和标签天线之间的通信。在目前射频识别系统中标签都是有芯的，但这类标签的结构复杂，体积、尺寸较大，价格较贵，所以限制了它的广泛应用。雷达技术的广泛深入地应用，激发了人们利用雷达技术进行射频识别的新思路。研究者又提出了无源无芯结构标签天线思想。Baum提出了奇点展开法的思想也促进了人们研究无芯标签的热情，奇点展开法对标签的散射场(雷达截面积)进行分析以提取目标的自然谐振频率。物体的本征频率的固有特性，即目标的奇点只与目标的结构有关，而与目标的位置、形态无关。每个物体的结构在平面波激励下都有自己的独特的散射场，通过分析物体的散射场，提取目标的固有频率并利用其进行存储和恢复数据就可以进行目标识别。因而标签的结构对于识别至关重要。为了寻求结构简单，易于实现的标签，Majid Manteghi and Yahya Rahmat-Samii等研究者研究了椭圆偶极子开槽方式。但这种方式，开槽数量有限。能够容纳的数据容量少，不能满足当前的需要。
本文也就是处于这点考虑并在前人研究的基础上，研究了能够具有较多开槽结构的标签结构，即蝶形结构。采用两个对称正三角形方式，能够开槽达到8个，容纳更多的数据容量。本文利用FEKO软件详细地分析这种蝶形标签结构在不开槽、开槽数量从一个到八个不同方向散射雷达截面。同时利用矩量法，提取了它的极点。这个研究的重要性在于改变传统的设计理念，彻底降低标签价格，推动射频识别技术的发展应用。

1 理论基础
在这一部分，主要介绍关于散射所涉及的理论知识，不作理论的探讨和推导，可参阅文献。
1．1 雷达散射截面
三维度单位体积内入射波段所携带的功率在全向辐射时，入射场强度为方向(θ，φ)的函数如图1所示，在定向方向上产生相同的散射功率密度可以表示为：

对于时谐电磁场，TEM模式电磁波，入射电场和磁场为(E，H)，坡印廷矢量可以表示为：

由式(3)和式(4)可以得到式(1)。
1．2 物体表面散射场积分方程
对于在自由空间里面积为S的任意形状的完纯导体，如图1所示。

当此导体受到已知强迫电流和磁荷(J，M)电场激励时，那么所有场将是具有时谐函数。在激励场已知，对完纯导体面积为S，设其表面电流为J，散射场为，这时整个区域的场为(E，H)。

上标带撇号和不带撇号的分别表示源的坐标和场的坐标。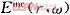为激励场的傅里叶变换，分别表示投射波的电场强度；J，M，ρ分别是等效源。如果只关心远场区，则上式可以简化为：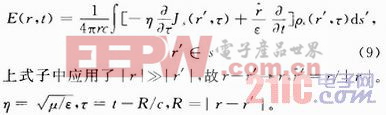


2 试验仿真和数据分析
下面给出具有对称性的边长为30 mm的两个对称正三角形构成的具有蝶形金属天线标签如图2(a)的雷达散射截面的仿真结果。完纯导体标签的雷达散射截面是频域的函数。当标签不开槽时，在激励源超宽带(UWB)脉冲的照射下，雷达散射是平滑的频域函数如图2(b)所示。当在金属标签上开槽时，那么标签的散射截面会出现凹点(极值点)。凹点所对应的频率，就是极值频率。这个极点的位置不但与标签的尺寸有关，而且与开槽的尺寸，位置，形状有关。利用FEKO仿真软件可以分析出开槽的位置，以及开槽的大小。通过分析得出通常开槽的大小一般取频率波长的1／4，或1／8可以获得较为理想的散射截面。本文给出了开槽数为零，即不开槽以及开槽数为8的散射截面。激励频率为2～10 GHz，开槽宽度为0．75 mm，开槽间距为1．732 mm方向为0°，30°，60°情况下的散射结果。表1给出了开槽数是8的具体参数。

图3(a)为槽数为8个的标签结构。图3(b)是激励平面波频率为2～10 GHz，0°极化，激励角度是0°，30°，60°情况下的散射场。图3(c)给出了90°极化的RCS和E场。

通过对表1中数据开槽大小、长度、槽的位置变化对极点的影响的仿真分析得出，当开槽较小，距离中心点位置较近时，将产生一个较高的约9 GHz频率极点。随着开槽长度的增加，极点频率越低并逐渐左移，开槽数量达到8个时，槽长最长，频率极点在5 GHz。本文是采用激励源UWB超宽带脉冲分别对极化方向为0°，90°两种极化方式做了仿真，从图3(c)，(b)中显示极化方向对极点的影响不明显，但在0°极化时，RCS幅度会发生约6 dB波动，而采用90°极化时，激励的入射方向对RCS几乎没有影响。结果显示该结构散射场极点稳定的特性。