扩频信号基于FFT码捕获的计算量分析

2 不同捕获方法的计算量比较
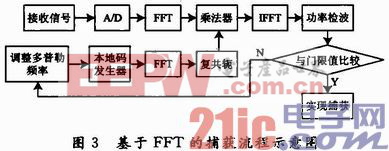
从理论上讲，滑动相关法与基于FFT的循环相关捕获法都是利用数据点进行相关计算并比较求得最大值。其不同之处在于计算量的差距上，采用基于FFT的循环相关法计算量大大的减少，下面对其进行分析。
2．1 传统滑动相关法
使用传统滑动相关法进行捕获，考虑21个多普勒频率分量，由于它们进行相同的操作，只对这21组数据的某一组进行讨论。
输入数据和C／A码各含有5 000个数据点，根据滑动相关法的原理，要将C／A码滑动5 000次，每滑动一次码片都要将C／A码与数据进行5 000点的复乘，这样，在每个频率分量上要进行5 000×5 000次乘法运算，则21个频率分量共进行：
S=5 000×5 000×21=5．25×108 (3)
次运算。由此可见，这种方法在硬件实现中非常浪费资源。
2．2 基于FFT的循环相关法
2．2．1 FFT算法计算量简介
采用快速FFT／IFFT运算，可以显著降低运算的复杂度，在这里简单介绍一下如何计算IFFT的运算量。FFT的运算量与此相同，不做赘述。
对于常用的基2IFFT算法来说，其复数乘法的次数仅为(N／2)log N。随着N的增加，算法复杂度之间的差距越明显，IDFT的计算复杂度会随着N的增加而呈现二次方增长，IFFT的计算复杂度的增加速度只是稍微快于线形变化。
对于计算点数比较多的系统，可以采用基4FFT算法。在4点的IFFT运算中，只存在与{1，-1，j，-j)的相乘运算，因此不需要采用完整的乘法器来实施这种乘法，只需要通过简单地加、减以及交换实部和虚部的运算(当与-j，j相乘时)来实现这种乘法。在基4算法中，IFFT变换可以被分为多个4点的IFFT变换，这样就只需要在两个级别之间执行完整的乘法操作。因此，N点的基4IFFT算法中只需要执行(3／8)·N·(log N-2)次复数乘法或相位旋转，以及N·log N次复数加法。
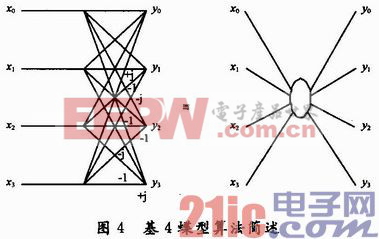
图4说明了4点的IFFT运算，称做基4蝶型运算。4个输入x0，x1，x2，x3经过简单的相加和相位旋转，生成4个输出y0，y1，y2，y3，例如y1=x0+jx1-x2-jx3。

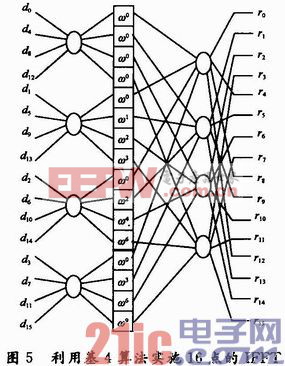
基4蝶型算法可以用于高效的计算大规模的IFFT。图5说明了利用基4蝶型算法实施16点的IFFT，其中包括2级运算，每级内包含4个基4蝶型运算，在两级之间存在中间过渡级别，用于对16个中间过渡结果实施相位旋转ωi，其中ωi=exp(j2πi／N)。在N=16的情况下，当i=0，2，4，8，12时，与ωi相乘就可以简化为与{1，-1，j，-j)相乘。

2．2．2 计算量分析
根据1．2．2节中介绍的循环相关捕获的具体步骤以及FFT算法的计算量，对基于FFT的循环相关捕获法计算量分析如下。
首先，根据式(2)将21个频率分量下的C／A码与射频相乘，需要运算次数为：
S1=21·N (4)
另外，N点基4FFT的运算量为(3／8)·N·(log N-2)，考虑21个多普勒频率分量以及FFT和IFFT双向变换，计算量为：
S2=2·21·(3／8)·N·(log N-2) (5)
因此，总的计算量为：
S=S1+S2=21·N·[(3／4)(log N-2)+1] (6)
这里数据点数N=5 000，则总计算量为915 180次，与滑动相关法相比，少了3个数量级。

3 结语
本文从扩频信号捕获的角度出发，描述了传统捕获方法和基于FFT的快速捕获方法的原理和步骤，并对不同捕获方法的计算量进行了分析和比较。在文中可以看到，基于FFT的循环相关捕获法其计算量比传统方法少了3个数量级以上，该方法在硬件实现中，与传统滑动相关法相比大大节省了资源，减少了耗时，是一种比较好的捕获方法。