m推演型声表面波高通滤波器设计

摘要：提出了一种新型m推演型梯形声表面波高通滤波器结构，给出了该结构的元件参数与滤波器频率响应指标参数之间的计算关系，并从滤波器传通截止条件和特性仿真两方面验证了该结构的正确性;基于单端对谐振器建模原理(模型)，在ADS中成功设计了一个截止频率为860MHz，极点频率为640MHz的m推演型声表面波高通滤波器，通带860~1400MHz内的插损小于4dB，阻带200~640MHz内带外抑制大于40dB。

梯形声表面波滤波器(Ladder-type Surface Acoustic Wave Filter，Ladder-type SAWF)以其插入损耗低、带内波动小、带外抑制强等特点，被广泛应用于雷达、通讯、导航、电子对抗等设备中。目前，学者们的研究大多集中在梯形SAW带通滤波器的设计和研制，对声表面波低通、高通、带阻滤波器的研究较少。

本文在m推演型LC高通滤波器的基础上，提出了一种m推演型梯形SAW高通滤波器结构，给出了该结构的元件参数与滤波器频率响应指标参数之间的计算关系，并从滤波器传通截止条件和特性仿真两方面验证了该结构的正确性。m推演型梯形SAW滤波器是由串臂上的单端对谐振器和并臂上的LC谐振回路组成，该滤波器在较宽的通带频率范围内具有较低的插入损耗。本文还基于单端对谐振器建模原理(模型)，在ADS中成功设计了一个截止频率为860MHz，极点频率为640MHz的m推演型SAW高通滤波器，860~1400MHz通带内插损小于4dB，200~640MHz阻带带外抑制大于40dB。

m推演型高通滤波器

结构

比较常见的高通滤波器类型有：常数k值高通滤波器和m推演型高通滤波器，常数k值滤波器的结构简单，频率响应由截止频率和阻抗特性决定。常数k值滤波器在阻带接近截止频率点处的衰减不大，而m推演型滤波器则可在阻带获得相对较大的衰减。

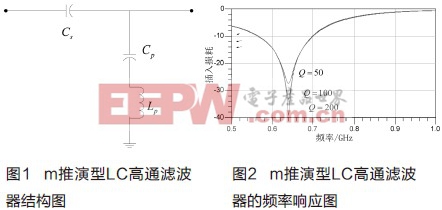
m推演型LC高通滤波器的结构如图1所示^[1]，它是由串臂上的电容C_s和并臂上电容C_p和电感L_p组成的串联谐振回路组成。C_s、C_P、L_p和m之间的相互关系如式(1)~(4)所示。

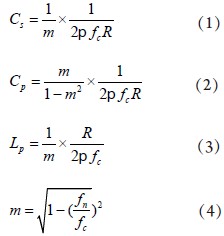
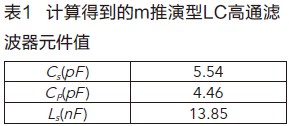
其中，f_c为滤波器截止频率，f_n为衰减极点所对应的频率点。特征阻抗R一般取50W。

仿真结果

m推演型LC高通滤波器的频率响应特性如图2所示，其中阻带截止频率为860MHz，衰减极点所对应的频率为640MHz，特性阻抗R取50W。经计算，图1中各元件值如表1所示。在实际应用中，电感的寄生效应不可忽略。寄生效应产生的电阻 的计算公式如式(5)所示：

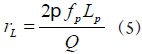
其中，Q为电感的品质因数。f_P为决定电感品质因数的频率，一般取截止频率f_c。

从图2中可以看出，随着品质因数的下降，通带内插损升高，阻带内插损下降。因为电感的品质因数通常为50~100，所以采用该结构很难实现低损耗、大衰减的滤波器。

m推演型梯形SAW高通滤波器

一级结构

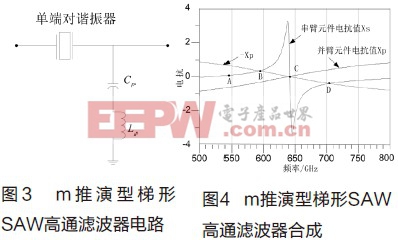
m推演型梯形SAW高通电路结构如图3所示。该电路由串联元件一个单端对谐振器和并联元件一个LC串联谐振回路组成。将单端对谐振器用作串联元件可以在反谐振频率附近产生大的衰减^[2]，在设计中，反谐振频率设置成极点频率f_n。

根据梯形滤波器的传通截止条件可知：当X_s>0且X_s<-X_p或X_s<0且X_s>-X_p时形成通带，当X_s<0且X_s<-X_p或X_s>0且X_s>-X_p时形成衰减带^[3]。SAW高通滤波器的电抗仿真曲线如图4所示，其中A，C点分别代表单端对谐振器的谐振频率和反谐振频率点^[4]，B、D点为满足X_s=-X_p的频率点。经分析可以得出，当滤波器工作频率低于A频率点时，形成衰减带，当滤波器工作频率在A和B之间时，形成通带，当滤波器工作频率在B和D之间时，形成衰减带，当滤波器工作在大于频率点D时，形成通带。当A、B频率点之间间隔较小时，就可以近似认为该滤波器为高通滤波器。

多级级联结构

多阶L型电路级联可以获得更大的衰减^[5]。四阶m推演型高通滤波器的结构如图5(a)所示，简化后的m推演型低通滤波器结构如图5(b)所示。因为单端对谐振器的插入损耗较大^[6]，所以用电容元件代替中间单端对谐振器，如图5(c)所示。因为C₁=C₂=C₃=C₄,L₁=L₂=_L3=L₄,所以，C_p=0.5C₁，L_p=2L₁。借助典型LCR模型仿真得到的四阶m推演型SAW高通滤波器频率响应如图6所示。

　　基于单端对谐振模型设计m推演型SAW高通滤波器

原理介绍

M推演型SAW高通滤波器主要是由单端对谐振器构成，滤波器的性能与滤波器结构、基板参数直接相关^[6]。在设计m推演型SAW高通滤波器时，基于SAW单端对谐振模型进行建模是一种简单、快速以及有效的方法。

SAW滤波器的基本元件是单端对谐振器，它的结构如图7所示。可以看出主要结构有以下几个部分：反射栅阵、叉指换能器以及叉指换能器和反射栅阵之间的间隙^[7]。利用ADS能够对叉指换能器、反射栅阵和叉指换能器和反射栅阵之间的间隙分别进行建模，包括利用动态电阻表示反射栅阵、梅森等效电路模型^[8]实现叉指换能器建模以及采用理想传输线表示反射栅阵与叉指换能器之间的间隙。采用以上几种手段实现单端对谐振器模型设计，单端对谐振器模型的ADS实现如图8所示。