通信系统中接收链的差分滤波器设计(上)

简介
     RF工程师在设计中常常会看到单端50 Ω系统。某些人 认为，差分电路很难设计、测试和调试。另一方面，为了提 高性能，通信系统常常要应用差分系统，尤其是IF级中。在 这些困难中，差分滤波器是一个关键问题。本应用笔记介绍 基本滤波器的一些重要规格概念、几类常用滤波器的响应和 切比雪夫1型滤波器应用，并且逐步说明如何将单端滤波器 设计转化为差分滤波器设计。本应用笔记提供了一个差分滤 波器设计示例，并讨论了关于如何优化差分电路PCB设计的 若干要点。
1 差分电路优点
本部分讨论RF信号链应用中差分电路相对于单端电路 的优点。
用户利用差分电路可以达到比利用单端电路更高的信 号幅度。在相同电源电压下，差分信号可提供两倍于单端信 号的幅度，以及更好的线性度和SNR性能。
差分电路对外部EMI和附近信号的串扰具有很好的抗扰
性。这是因为接收电压加倍，噪声对紧密耦合走线的影响在 理论上是相同的，因而它们彼此抵消。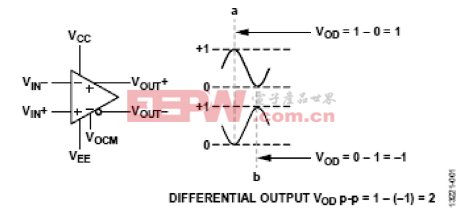

图1   差分输出幅度
差分信号产生的EMI往往也较低。这是因为信号电平的变化（dV/dt或dI/dt）产生相反的磁场，再次相互抵消。差分信号可抑制偶数阶谐波。例如，让连续波(CW)通 过一个增益级。若使用一个单端放大器，如图2所示，输出可表示为公式1和公式2。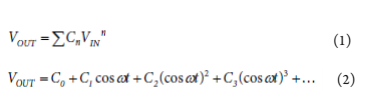

其中?表示该序列一直进行下去。若使用一个差分放大器，则输入和输出如图3所示，表 示为公式3、公式4、公式5和公式6。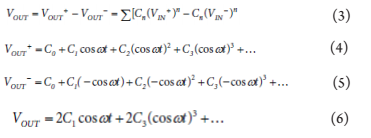

其中?表示该序列一直进行下去。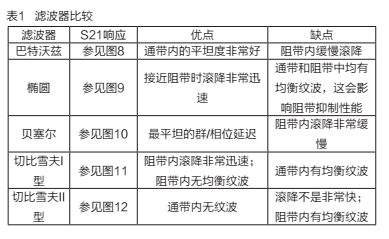

理想情况下，输出没有任何偶数阶谐波。
因此，在通信系统中，为了实现更好的性能，差分电 路是首选。

图2  单端放大器    

图3  差分放大器
2 滤波器
2.1 滤波器规格
截止频率、转折频率或拐点频率是系统频率响应的边 界，此时流经系统的能量开始减少（衰减或反射），而不是 自由通过。
带内纹波指通带内插入损耗的波动。
相位线性度指相移与目标频率范围内的频率成比例的 程度。
群延迟衡量一个穿过受测器件的信号的各种正弦成分 幅度包络的时间延迟，它与各成分的频率相关。

3  滤波器比较

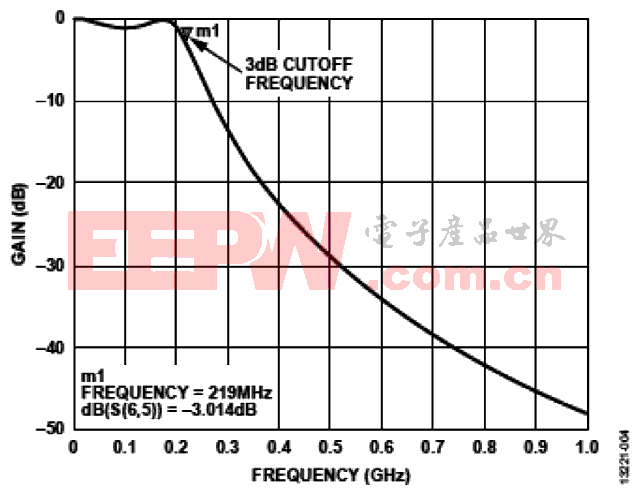
图4   3 dB截止频率点

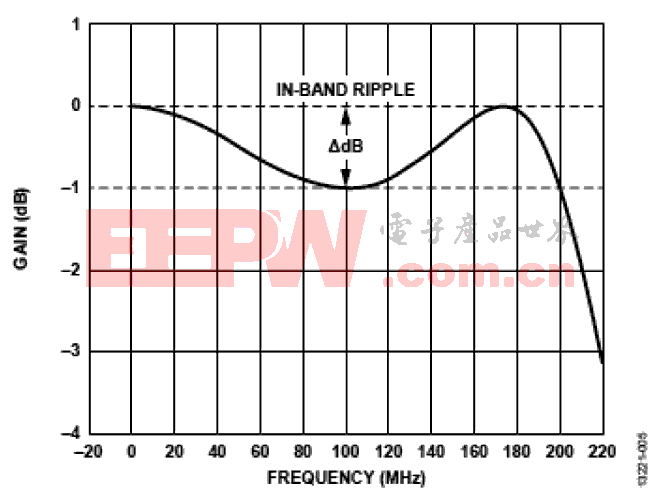
图5   带内纹波

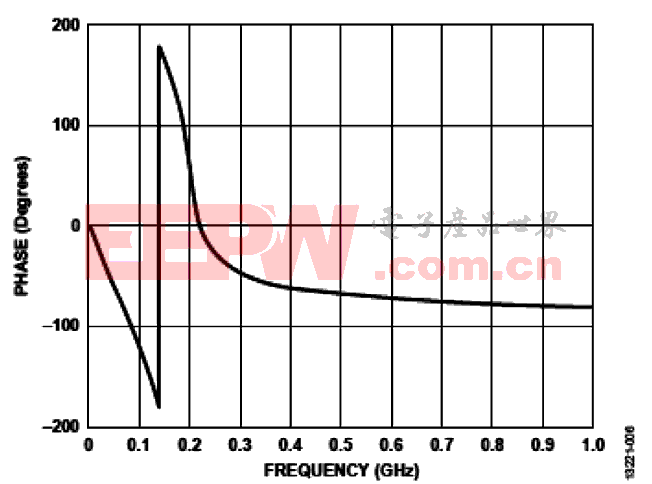
图6  相位线性度

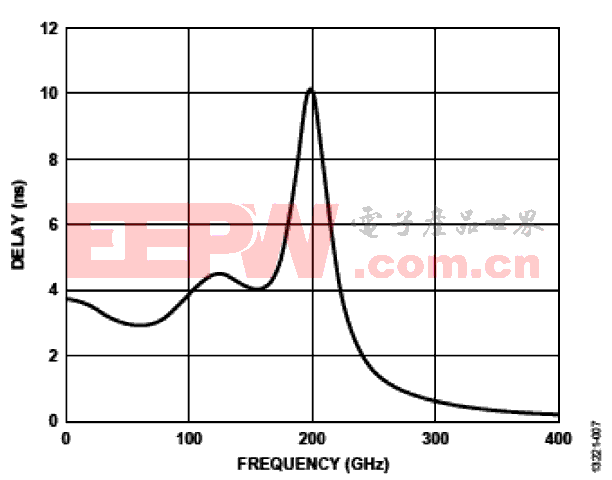
图7   群延迟        

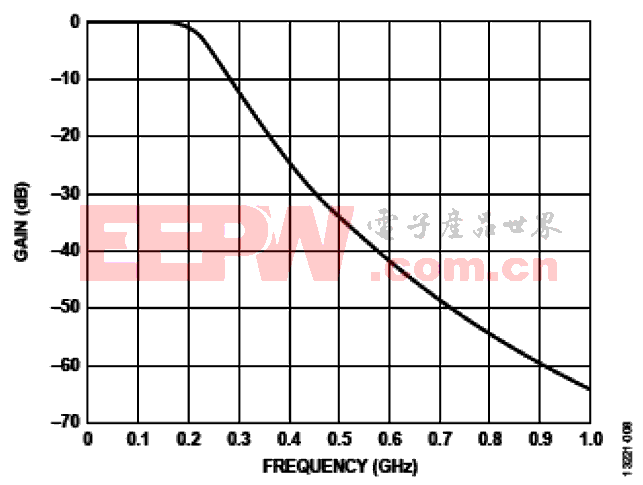
图8  巴特沃兹滤波器S21响应

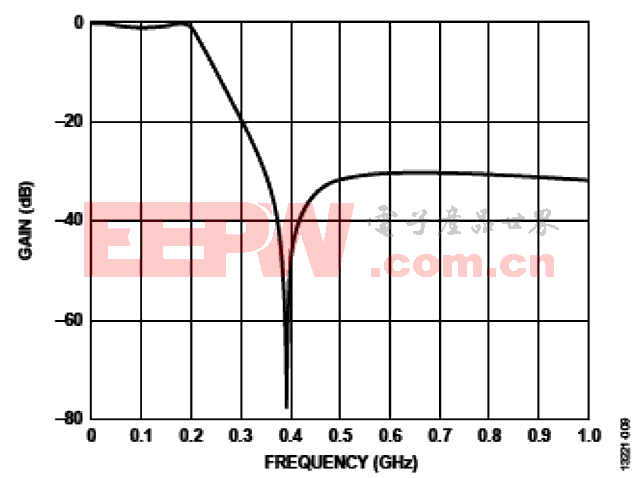
图9  椭圆滤波器S21响应
通信接收链中设计的IF滤波器基本上是低通滤波器或带通滤波器，用于抑制混叠信号以及有源器件产生的杂散。 这些杂散包括谐波和IMD产物等成分。利用该滤波器，接收 链可提供干净且具有良好SNR的信号供ADC分析。切 比 雪 夫 I 型 滤 波 器 具 有 良 好 的带内平坦度，阻带内滚降迅速且无均衡纹波，因而选择它作为拓扑 结构。

4 低通滤波器设计
接收IF滤波器用于抑制杂散和混叠信号，因此阻带滚 降越快越好，但更快的滚降意味着要使用更高阶器件。尽管 如此，但不推荐使用高阶滤波器，原因如下：
? 在设计和调试阶段调谐困难。
? 量产困难，因为电容间和电感间存在差异，各PCB上 的滤波器难以具有相同的响应。
? PCB尺寸较大。
一般使用七阶或更低阶的滤波器。另一方面，当器件 的阶数相同时，若更大的带内纹波不是问题，则可以选用更 快的阻带滚降。
所需的响应通过指定选定频率点需要的衰减来定义。

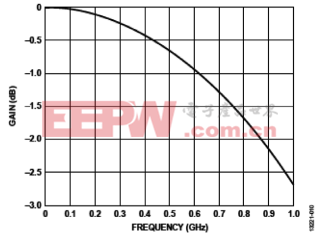
图10  贝塞尔滤波器S21响应          

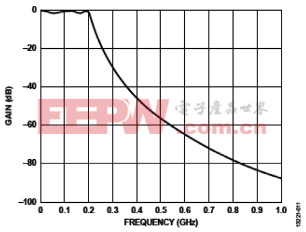
图11  切比雪夫I型滤波器S21响应

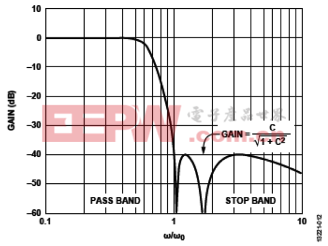
图12  切比雪夫II型滤波器S21响应

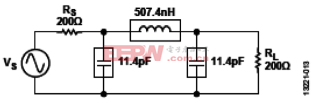
图13  单端滤波器示例      

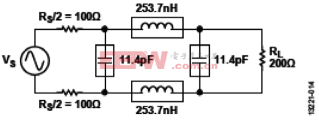
图14  单端滤波器转化为差分滤波器

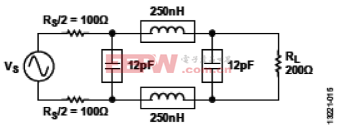
图15  最终差分滤波器
为了确定通带中的最大纹波量，应使该规格等于系统要求的最大限值，这样有助于获得更快的阻带滚降。
使用低成本滤波器软件， 如MathCad?、 MATL AB?或ADS来设计单端低通滤波器。或者手动设计滤波器。Chris Bowick所著《RF电路设 计》提供了很有用的指南。为了确定滤波器的阶数，应将目标频率除以滤波器的 截止频率，使其归一化。

例如， 若要求带内纹波为0.1 dB， 则3 dB截止频率为
100 MHz。在250  MHz时，要求抑制性能为28 dB，频率比 为2.5。三阶低通滤波器可满足这一要求。如果滤波器的源阻抗为200 Ω，滤波器的负载阻抗也是200 Ω，则RS/RL为
1； 使用电容作为第一元件。 这样用户获得归一化的C1 =
1.433，L2 = 1.594，C3 = 1.433；fc为100 MHz，使用公式7和 公式8获得最终结果：

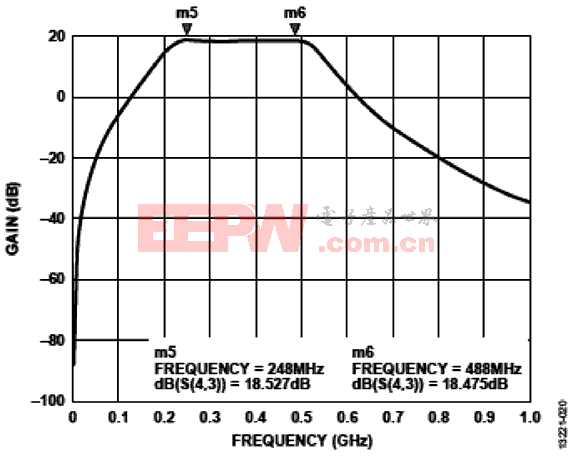
图16   采用理想电感的滤波器传输响应    

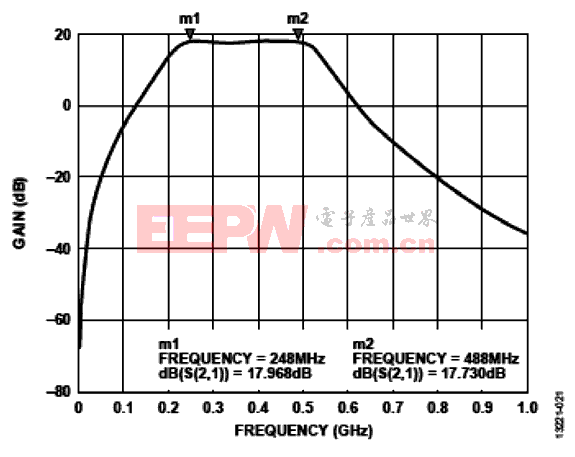
图17   采用Murata LQW18A电感的滤波器传输响应

其中：
CSCALED 为最终电容值。 LSCALED 为最终电感值。 Cn 为低通原型元件值。 Ln 为低通原型元件值。 RL 为最终负载电阻值。 fc 为最终截止频率。
C1SCALED = 1.433/(2π × 100 × 10 × 200) = 11.4 pF
L2SCALED = (1.594 × 200)/(2π × 100 × 10 ) = 507.4 nH
C3SCALED = 11.4 pF
电路如图13所示。
将单端滤波器转化为差分滤波器（参见图14）。
对各元件使用实际值，更新后的滤波器如 图15所示。
注意， 如果混频器或IF放大器的输出阻抗 以及ADC的输入阻抗为容性，则考虑使用电容 作为第一元件和最后元件会更好。另外，第一电 容和最后电容的容值调谐速率（至少0.5 pF）必 须高于混频器或IF放大器的输出阻抗以及ADC输 入阻抗的容值。否则，调谐滤波器响应将非常困难。 （未完待续）