连接在线路中间的容性负载

图4.22说明了一条长线中间挂了一个电容的情形。一个从左边进入的信号遇到电容后一分为二，一部分信号后向射，另一部分经过电容继续向前传播。

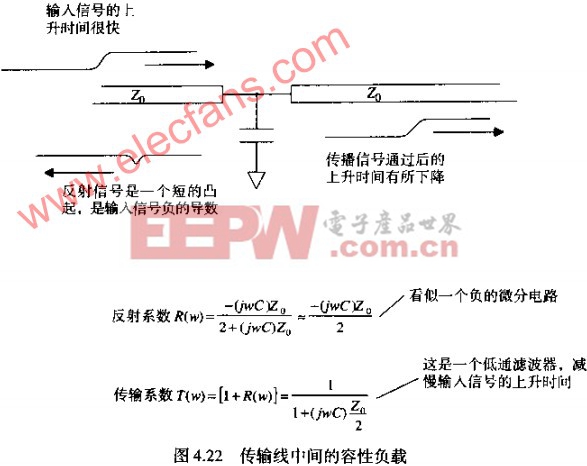
这个问题棘手的方面在于反射系数是频率的一个函数。我们将分别来估算反射信号的大小以及对传播信号的影响。

1、容性负载上的信号反射

像其他反射问题一样，我们试着用反射方程式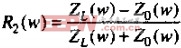（）来分析。这个方程需要我们指定线路和端接在阻抗，目前用传输线阻抗Z0作为端接阻抗。

图4.22中传输线在左边部分终止于这个电容，其总的端接负载等于电容的电抗与其余线路输入阻抗的并联值。如果不知道在右边线路端接情况，可以对输入阻抗进行一些假设。那么，如何计算出总的端接负载呢？

为了解决这种进退两难的困境，首先假设我们正在处理是一条低损耗的线路，进一步假设右边的线路是末端端接的，因此它的输入阻抗等于Z0=（L/C）1/2，与频率无关。同样地，我们还可以假设右边的线路非常长，从而使得远端反射回来的信号由于到达太迟而不会影响由容C引起的直接反射。无论是哪种情况，我们都将假定右端的输入阻抗等于ZO。

现在我们可以用电容C和ZO的并联结果替换式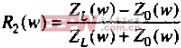（）中的ZL项。化简并重新整理各项，得到容性负载反射系数结论：

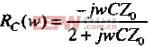
当频率高于FMAX=（CZOπ）-1时，几乎是完全反射。不要将传输线使用在该频率以上。当频率在FMAX以下时，反射系数则有所区别，它实际上返回上个脉冲，等于输入阶跃的导数。微分常数等于-C（ZO/2）。

如果数字转折频率是在FMAX以下，那么可以估算反射脉冲的峰值的峰值振幅：

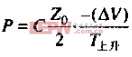
其中，△V=输入电压阶跃的大小
P=反射脉冲振幅，V
T上升=输入信号的10~90%上升时间，S
C=负载电容，F
ZO=高频线路阻抗，（L/C）1/2

2、信号通过一个容性负载

假设两边的线路都很长，因而在短时间内，从电容看过去，其有效阻抗都等于ZO=（L/C）1/2。这个假设使得我们能很快地计算出传输系数：

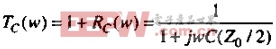
这是一个时间常数为C（ZO/2）的低通滤波器的方程，这个阶跃响应的10~90%上升时间应该为时间常数的2.2倍，或者是：

容性负载使通过它的传播信号的上升时间劣化，采用式（）可以算出传播信号的上升时间。它综合了输入的上升时间和电容上升时间，以算出输出的上升时间。

如果符合以下条件之一，则本文的近似值成立：

1、传输线在两个方向都端接。

2、传输线的长度大于上升沿的有效长度（在两个方向）。

当低阻抗驱动器与负载电容连接靠得太近时，从电容端来看，有效驱动阻抗将降低，最终结果是反射更小，以及上升时间的畸变更小。