|
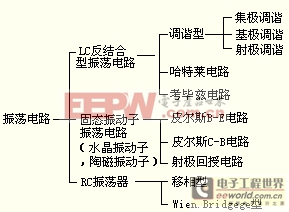
表1 振荡电路的分类
(在实验之前,将振荡电路先分类,较容易理解。此表按根据决定振荡频率的元件与电路形式分类。)
|
其中的RC振荡电路是由电阻与电容所形成的调谐电路,因此,无法产生高谐波,不适合高频振荡电路。高频振荡电路一般使用LC振荡电路,也即固态振荡电路。
本章将经由这些高频率振荡电路的设计、制作,而了解其工作原理与过程。
|
 振荡电路的工作原理
振荡电路的工作原理
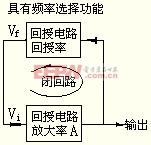
图1所示的为振荡电路的工作原理说明。
振荡条件为
(1)回授的信号Vf与输入信号为同相。
(2)经过闭回路后,信号会增大,也即Aβ>1。
|
图1 振荡电路的原理
(由此一方框图可以知道发生振荡的原因是同一信号经过放大电路与正回授电路而产生的)
|
首先,将电源加在振荡电路上,在电源或振荡电路内发生微小的杂讯。此一杂讯经过放大电路放大,成为输出信号。然后,此一输出信号的一部分经过回授电路再输入放大,便形成振荡信号。
在此,如果Vf的相位与输入信号Vi为同相,信号便会在闭回路内旋转,此为持续振荡的条件之一。另外,在回授电路中,如果具有选择频率的功能,便能够只针对特定的频率回授。
将以上的工作过程整理后整理,其动作为放大器输出—回授电路—放大器输入—放大器输出———...
如果要满足振荡持续,其条件为:
(1)由反馈电路所反馈的信号与输入信号为同相……正反馈。
(2)经过闭回路后,信号逐渐增大……Aβ>1。
振荡电路由于所使用的反馈电路不同,而可以分为许多种类。
 振荡电路的特性
振荡电路的特性
在设计振荡电路时,必须注意以下的特性。
▲频率稳定度
振荡电路特性的良否,是由频率稳定度决定的,此为振荡器的重要特性。关于频率的变动可以用以下数值表示之。
频率:经过时间的变动
电源ON后,随着时间的经过,所产生的频率变动。特别是,在热机(warm-up)时的变动最大。
频率温度系数
相对于温度变化时的频率变动,用ppm/℃表示。
频率:电源电压变动
电源电压变化时的频率变动,用%/V表示。
▲输出位准的稳定度
相对于时间,温度,电源电压的输出位准稳定度。
▲振荡波形失真
此为正弦波输出的失真率表示。如果为纯粹的正弦波时,失真率成为零。
在高频率振荡电路中,除了上述特性以外,尚要考虑到在设计时的频率可变范围以及振荡频率范围。
|