R(d)=asexp(-d2/b2)+(1-as)exp(-d/c) (3)
其中，as(0
as1)为快起伏分量在总能量中所占的比例，b、c分别是快、慢起伏分量的去相关距离.这些参数的取值依不同的地物、工作频率和天线极化方式而不同.
从时间特性角度考虑，Aq与具有相似分辨单元尺寸的常规脉冲雷达体制下的杂波回波幅度具有相同的时间起伏特性.根据以往的测试研究，在X波段且对于适中的分辨单元尺寸，概率密度分布满足瑞利分布.一般地物的相关函数特性则也是包含了快起伏和慢起伏两种尺度的变化，其归一化时间相关函数为：
R(τ)=atexp(-α2τ2)+(1-at)exp(-βτ) (4)
其中，at(0at1)为快起伏分量在总能量中所占的比例，α、β分别是快、慢起伏分量的去相关时间.
因此，模拟PRC-CW雷达的地杂波回波信号的步骤为：
(1)产生一组长度为Q的随机序列［4］，它的概率密度分布满足Weibull分布，而相关性满足式(3)；
(2)以上一步产生的Q个数据，作为各子波束回波幅度时间序列的均值mq,从而模拟产生Q组具有式(4)相关特性的相干高斯随机序列，作为各子波束的回波复振幅时间序列；
(3)根据式(1)进行迭加，从而得到Vg(t).
但是，这样产生的地杂波回波信号尽管考虑到了不同子波束间的空间相关性和同一子波束的时间相关性，但不同子波束间的时间相关性却被认为是互不相关的，这与实际情况有差异，只是时间特性上的一种极端情况.那么，另一种极端情况就是完全相关，而实际情况应介于这两种情况之间.所以，也要考虑完全相关情况下地杂波回波信号，产生步骤是：
(1)产生一个子波束的回波复振幅时间序列，它的实部和虚部是相互独立的、但各自满足式(4)相关特性的相干高斯随机序列；
(2)在上一步产生的时间序列的基础上，考虑距离衰减，利用式(2)，即可得到Q个子波束的时间序列；
(3)根据式(1)进行迭加，从而得到Vg(t).
三、地杂波的时间起伏频谱特性
Vg(t)的相关函数为：
RV(τ)=RXX(τ)+RYY(τ)+j［RYX(τ)-RXY(τ)］ (5)
假定Vg(t)可看成是一广义平稳窄带过程，且回波信号的功率谱是一对称谱，则有：RXX(τ)=RYY(τ),RYX(τ)=RXY(τ)=0.所以，RV(τ)=2RXX(τ)，归一化得到相关系数为：rV(τ)=RXX(τ)/RXX(0).对于PRC-CW雷达，发生码元迭加时其相关函数特性，分以下两种情况进行讨论.
1.不同波束在时间特性上是相互独立的
假定xi、yi、zi、…，(i=0,1,2,…,N-1)分别代表不同波束的回波信号，i代表时间序列中的序号，并且，xi、yi、zi，…，是独立同分布的高斯N(0，σ2)随机变量，有：
E［x2i］=E［y2i］=E［z2i］=…=R(0);
E［xixi+τ］=E［yiyi+τ］=E［zizi+τ］=…=R(τ);
=E［xizi］=E［yizi］=E［xiyi+τ］=E［xizi+τ］
=E［yizi+τ］=…=0
不失一般性，只考虑三个码元迭加后的情况，即：Ai=xi+yi+zi,(i=0,1,…,N- 1)，则：
E［A2i］=E［(xi+yi+zi)2］=3R(0);
2.不同波束在时间特性上是完全相关的
假定xi、yi、zi，…(i=0,1,2,…,N-1)分别代表不同波束的回波信号,i代表时间序列中的序号，并且，xi、yi、zi，…是完全相关的同分布的高斯N(0,σ2)随机变量，有：
E［x2i］=E［y2i］=E［z2i］=…=R(0);
E［xixi+τ］=E［yiyi+τ］=E［zizi+τ］=…=R(τ);
E［xiyi+τ］=E［yizi+τ］=E［xizi+τ］=…=R(τ);
Q个码元迭回后的序列为:
Ai=xi+xi+1+xi+2+…+xi+Q-1,i=0,1,…,N-1
则E[A2i]=QR(0)+2(Q-1)R(1)+2(Q-2)R(2)+…+2R(Q-1)；
E［AiAi+τ］=QR(τ)+(Q-1)R(τ+1)+(Q-2)R(τ+2)
+…+R(τ+Q-1)+(Q-1)R(τ-1)
+(Q-2)R(τ-2)+…+R(τ-Q+1).
仍对相关函数进行归一化，并与没有发生码元迭加时的归一化相关函数相比较：m=E［AiAi+τ］/E［A2i］-R(τ)/R(0).求解此解析式，可得：
如果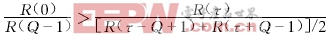
成立，则迭加后的相关性将增强，反之，相关性将减弱.分析脉冲雷达的时间相关特性，可知上述不等式都是成立的，所以，在有码元迭加的情况下，如果不同波束间是完全相关时，则时间相关性将增强，且增强的程度取决于上述不等式的差异.
因此，对于PRC-CW雷达而言，由于码元和码元之间既不可能完全独立，又不可能完全相关，而是介于其中，所以其时间相关特性也应介于上面两种极端情况之间，也就是说，当码元回波发生迭回时，其时间相关性总是要增强的.
通过对相关函数作傅立叶逆变换或利用AR模型，就能得到信号的功率谱密度［5］.
四、地杂波相关特性仿真结果
实验中对多种典型地物在PRC-CW雷达下的回波信号进行了计算机模拟，图3～图6分别示出在不同条件下的裸土和油菜的功率谱曲线，它们的空间分布参数及相应的空间相关系数参数、时间相关系数参数列于表1中，采样时间为25微秒.针对不同雷达工作参数得到不同的回波码元迭加次数，进行模拟得到PRC-CW雷达发生码元迭加时的地杂波回波复振幅序列Vg(t)，再分析其频谱特性.
|
