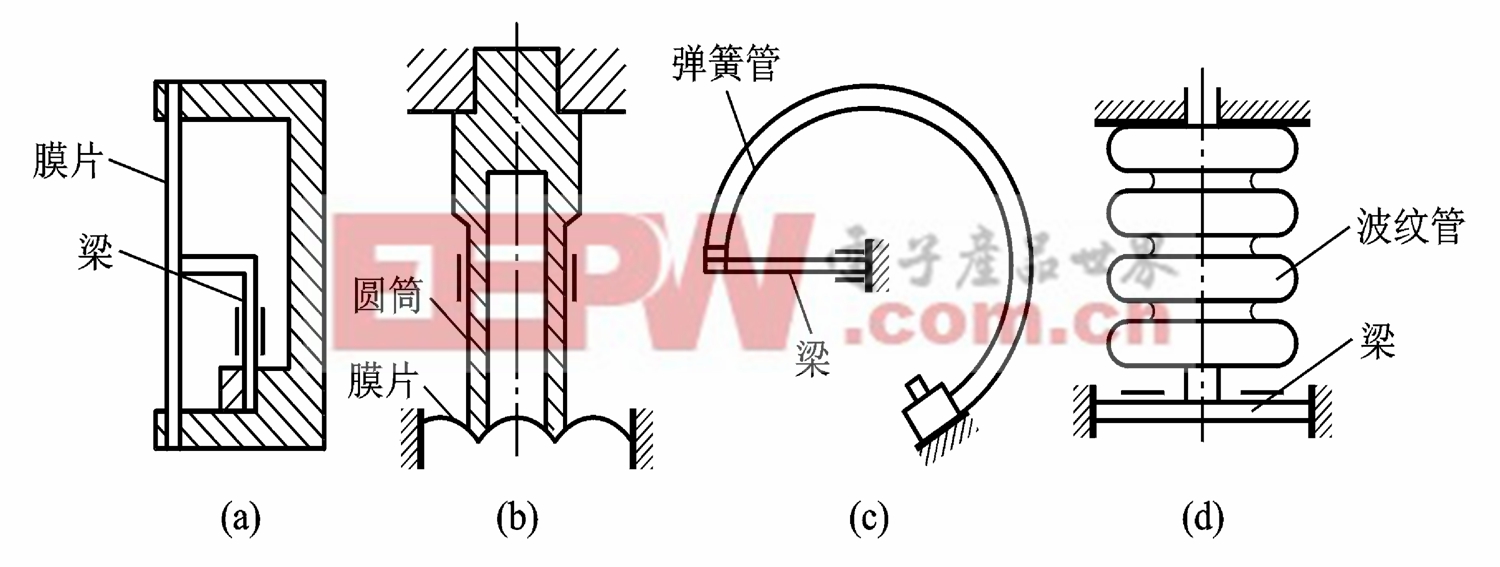
弹性敏感元件的基本特性

弹性敏感元件的基本特性

　　

　　 作用在弹性敏感元件上的外力，引起弹性敏感元件相应的变形（应变、位移、转角

等），它们之间的关系可用以下特性指标表示。

　　1．刚度。 刚度是弹性敏感元件在外力作用时抵抗变形的能力，一般用k表示，其定

义式为
　　　　　　　　　　　　　　　　　f　　（4.2.1）

式中F为作用在弹性敏感元件上的外力，x为元件在外力作用下产生的变形。

　　 2．灵敏度。 灵敏度表示在单位外力作用下产生变形的大小，灵敏度是刚度的倒

数，一般用S表示

　　　　　　　　　　　　　　　　　　　　　　（4.2.2）

　

　　3．弹性滞后。 弹性滞后是指弹性敏感元件在弹性变形范围内，加载、卸载正反行

程曲线不重合的现象，一般用最大变形滞后与最大载荷下的总变形的百分比表示。产生

弹性滞后的原因主要是由于弹性敏感元件在工作时分子间存在内摩擦，这种滞后误差将

会造成测量误差，因此必须选择弹性滞后小的弹性敏感元件。

　　 4．弹性后效。 弹性敏感元件的变形不仅随载荷变化，而且与时间有关。当所加载

荷改变时，不是立即完成相应变形，而是经一定时间间隔逐渐完成变形，这一现象称为

弹性后效。弹性后效的存在使得弹性敏感元件的变形不能迅速随外力的改变而变化，造

成测量误差，在动态测试时，这种现象更加严重。

　　 5．温度特性。 环境温度的变化会引起弹性敏感元件的热膨胀现象，通常用线膨胀

系数at表示。时的长度，则温度为t℃时的长度为

　　　　　　　　　　　　　　　　　　　 （4.2.3）

　　 温度的变化也会引起弹性敏感元件材料的弹性模量E的变化，一般来说，弹性模量

随温度的升高而降低，变化的大小用弹性模量温度系数（为负值）表示，若E0表示温

度为时的弹性模量，则温度为t℃时的弹性模量为

　　　　　　　　　　　　　　　　　　　（4.2.4）

　　 弹性敏感元件的几何尺寸和弹性模量随温度的变化，必然会引起测量误差，这在设

计传感器时必须加以考虑，甚至采取补偿措施。

　　6．固有频率。 弹性敏感元件的固有频率决定其动态特性。一般来说，固有频率越

高，其动态特性越好。固有频率的理论计算比较复杂，实际中常常通过实验来确定，也

可用下式估算

　　　　　　　　　　　　　　　　　　　　　　（4.2.5）

式中k为弹性敏感元件的刚度，me为其等效振动质量。

　　 由上式可见，弹性敏感元件的固有频率和灵敏度之间存在相互矛盾问题，提高灵敏

度，会降低固有频率，使动态特性变差，反之亦然。因此必须根据具体要求综合考虑。

　　 7．机械品质因数

　　 对于作周期振动的弹性敏感元件，由于阻尼的存在，每一个振动周期都伴有能量消

耗。

　　 机械品质因数定义为每个振动周期存储的能量与由阻尼等消耗的能量之比，即

　　　　　　　　　　　　　　　　　　　　　　　（4.2.6）
式中Es——每个振动周期存储的弹性应变能量；

　　Ec——每个振动周期由阻尼等消耗的能量。

　　 对于小阻尼系统(ξ 1)，机械品质因数就等于其谐振状态下的振幅比，即

　　　　　　　　　　　　　　　　　　　　　（4.2.7）

式中A0为静态振幅，A为谐振状态下的振幅，ξ为阻尼比。

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　　 由上述分析，弹性敏感元件的机械品质因数Q值反映了其消耗能量快慢的程度，也

反映了其幅频特性曲线陡峭的程度。弹性敏感元件的阻尼比越小，机械品质因数Q值越

大，这时弹性敏感元件消耗的能量越少，系统的储能效率就越高；同时系统的幅频特性

越陡峭，工作频带变窄。这就意味着弹性敏感元件用作谐振元件的选频愈强，谐振频率

愈稳定，这对设计谐振式传感器有实际意义。只有选用品质因数高的弹性敏感元件，设

计制造出高Q值的谐振元件，才能构成高性能的谐振式传感器。