如何选择谐振杆的尺寸使功率容量达到最佳

随着行业的发展，功率和互调要求成为越来越多产品的瓶颈，因此，产品的功率和互调指标的好坏越来越成为衡量一个滤波器设计生产企业的技术水平的关键参数。本文主要针对在一定的单腔尺寸的前提下如何选择谐振杆的最佳尺寸，使得其功率容量达到最佳状态。

我们首先来分析一个单腔里面的电场分布及其强弱。众所周知，一个谐振单腔内的电场主要分布在谐振杆上表面与盖板、谐振杆内壁与调谐螺杆外表面之间，其他地方的电场很弱。在有功率通过该谐振单腔的时候，电场最强点是限制该单腔功率容量的关键点， 因此解决功率问题的关键就是想办法降低电场最强点的电场强度。

现在我们就寻找一般情况下单腔里面的电场最强点在何处？假设单腔大小为a*b*c，谐振杆外半径为Rout，内半径为Rin，调谐螺杆半径为Rsc，则调谐螺杆与谐振杆内壁之间的距离d1＝Rin-Rsc，谐振杆盘面与盖板距离为d2。众所周知，单腔在谐振情况下电场主要分布在两块区域：谐振杆盘面与盖板之间、谐振杆内壁与调谐螺杆之间，必要时还需要考虑到谐振杆盘与侧壁之间的电场（单腔较小频率较低时） 。由于"木桶"效应，单纯增加一个区域的功率容量（就是降低这个区域的电场强度）是不能起到增加单腔功率容量的目的的，要同时使两个区域的电场强度都比较小，才能使单腔更不容易打火。

首先考虑谐振杆盘面与盖板之间的电场， 如图可以看见某个时刻谐振杆盘面与盖板之间的电场分布。

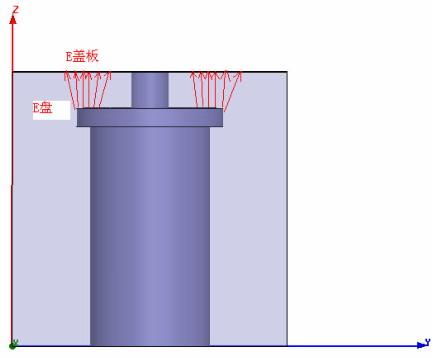
由图可见，1.当频率较低（低于900M），谐振杆盘较大时，盖板上的电场与盘面的电场几乎一样；

2.当频率较高（高于1.8G），谐振杆盘面较小时，盘表面的电场会比盖板面上的电场强，两者的倍数关系与谐振杆盘面的大小有关。

再考虑谐振杆内壁与调谐螺杆之间的电场，下图表示在某个时刻该区域的电场分布。

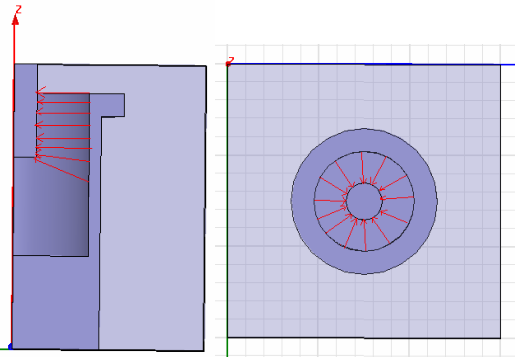
由图可见，纵向上该区域电力线基本上是平均分布的，但在横向上，电力线的分布明显不均匀，越靠近调谐螺杆表面，电力线越密集，也就是电场越强。在调谐螺杆表面， 电场最强。 因为谐振杆内壁的电力线几乎都中止在调谐螺杆表面，因此两者的电场有如下关系：E 内壁（Ein）*S 内壁（Sin）＝E 螺杆（Esc）*S螺杆（Ssc），Esc/Ein＝Sin/Ssc＝2*pi*Rin/2*pi*Rsc＝Rin/Rsc。即两者电场之比为两半径之比的倒数。

从上面的分析可以看出， 两个区域电场最强的点分别在谐振杆上表面和调谐螺杆表面。 在此我们分析这两者之间的关系， 当这两个电场最强点的电场相等时，这两块区域就同时达到了最大的功率容量，因此该单腔就能达到最大的功率容量。假设某个时刻谐振杆与盖板之间的电位差为V，则电场沿谐振杆盘面到盖板面的线积分和沿着谐振杆内表面到螺杆表面的线积分相等，均为V。考虑两种情况：

1. 频率较低，谐振杆盘面较大时，谐振杆盘面到盖板间的电场强度为恒定值Eup，则V＝Eup*d2＝（Esc+Ein）/2*d1，Eup*d2＝（Rsc/Rin*Esc+Esc）/2*d1＝Esc*（Rsc+Rin）/（2Rin）*d1两区域最大电场相等，则，Eup＝Esc，d2＝（Rsc+Rin）/（2Rin）*d1上式即为该条件下要使单腔功率容量最大所需要满足的等式。

举个例子，谐振杆盘面距离盖板3mm，调谐螺杆直径为4mm，由上面的等式我们可以计算得到内径的最佳值。

3＝（2+Rin）/（2Rin）*（Rin-2）

得到Rin＝6.6mm（约），即谐振杆内径最佳值为13.2mm。

注：上面各等式均要求在满足单腔谐振频率的要求。

2. 频率较高，谐振杆盘面较小，此时谐振杆盘面到盖板间的电场强度不恒定，假设谐振杆盘面电场为Ecp，盖板面电场为Etop，我们还是假设两电场的平均电场强度为Eup，则Ecp>Eup，而Ecp＝Esc，则此时需满足：

d2>（Rsc+Rin）/（2Rin）*d1

因此，在上面的例子中，如果谐振杆盘面很小，则谐振杆内径最佳值应为Rin略小于6.6mm。

从上面的分析我们可以得出结论：

1.  频率较低，谐振杆盘较大时，我们要尽量想办法拉大谐振杆盘与盖板间的距离，同时，要尽量满足以下等式：d2＝（Rsc+Rin）/（2Rin）*d1，否则，调谐螺杆易打火。

2.  频率较高时，我们要尽量把谐振杆的盘加大，尽量使谐振杆盘面上的电场均匀，同时满足d2>(Rsc+Rin)/(2Rin)*d1。

3.  同时，我们也可以根据等式d2＝（Rsc+Rin）/（2Rin）*d1 分析在极限功率下使谐振杆盘先打火还是螺杆先打火。d2>(Rsc+Rin)/(2Rin)*d1,则为螺杆先打火，d2<(Rsc+Rin)/(2Rin)*d1,则为谐振杆盘面先打火。

4.  如果已经出现打火，改进功率时，不能一味的加大谐振杆与盖板之间的距离，因为如果不改进谐振杆内径尺寸，调谐螺杆一样容易打火。