基于介质集成波导(SIW)的三路 零相位功率分配/合成器
1 引言
近年来,介质集成波导(SIW)技术被提出并且迅速发展。作为一种新型的传输线结构,它综合了传统矩形波导和微带线的一系列优点:和传统的矩形波导一样,SIW具有较高的品质因数和很小的辐射损耗;和微带线一样具有体积小、重量轻、容易加工和集成等优点。从工作原理上看,能够用普通波导实现的结构也都可以用SIW来实现,比如滤波器、天线、微带到波导的过渡、耦合器、功分器等。
功率分配/合成器是一种重要的微波毫米波元件。在多普勒体制的和差三路式单脉冲雷达中,各路混频器所需要的本振功率通常用一个三等分功分器从雷达频率合成器上获得。设计功分器最常用的方法是采用树状结构,先把输人信号分成两路,然后每路又分成两路。这种结构分的路数需满足2*N (N= 1, 2...),如要分成3路,则必须先分成4路,其中一路用匹配负载吸收。这种方法不但白白耗费了一路能量,而且由于其它3路负载与吸收支路匹配负载并不完全一样,因而其平衡度也不理想。另一种方法是先用一个功率比为1:2的功分器,然后在功率输出较大的一路接一个二等分功分器。这样既可以做到等分功率,又可以避免不必要的吸收,但在电路中,实现满意的1:2功率分配并不容易。本文采用基于SIW的三路零相位功率分配/合成器设计,可以克服上述困难,并且它的驻波比小,插入损耗小,不平衡度小,各路间隔离度高。
2 理论分析
2.1 SIW的原理
SIW的原理是在微波毫米波介质基片上制作两排周期性金属化通孔,这样在上下金属面和两排金属化通孔之间就形成了一个类似于矩形金属波导的集成导波结构,如图1所示。当金属化通孔之间的间距满足一定条件时,电磁场被限制在导波结构内,而且传输类似于普通矩形金属波导内的模式。

图1 介质集成波导(SIW)
由于介质集成波导中的TE10模与传统矩形波导中的TE10模非常相似,因此我们可以利用传统矩形波导和介质集成波导的等效关系来确定介质集成波导的最初几何尺寸。
 (1)
(1)
其中 是归一化系数,
是归一化系数, 是相对应的矩形波导的宽度,
是相对应的矩形波导的宽度, 是SIW的宽度,d是孔的直径,p是相邻两个孔的中心间距。
是SIW的宽度,d是孔的直径,p是相邻两个孔的中心间距。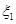 、
、 和
和 定义为:
定义为:
 (2)
(2)
 (3)
(3)
 (4)
(4)
图1中,两排金属孔间的距离a决定了波导的工作频率。孔的直径d应该小于等于工作最大波长的十分之一,孔心距p小于等于二倍孔直径。
2.2 三路零相位功率分配/合成器原理
如图2所示,作功率分配器时,①端口为输入端口,②、③、④端口为三路输出端口,⑤、⑥端口为隔离端口。通过调整金属化通孔带L1、L2、L3、L4和间距g1、g2、g3的大小来改变耦合量,从而得到所需的功率分配、回波损耗和隔离度;反之,作功率合成器时,②、③、④端口为三路输入端口,①端口为输出端口,⑤、⑥端口接匹配负载。图2中,由于从端口①到端口②、③、④信号传输的路径不同,引入了一段L5来调节三路的相位差,使之为零相位。
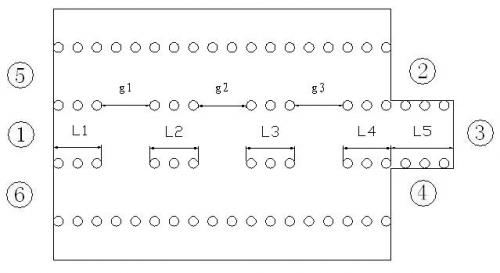
图2 三路零相位功率分配/合成器示意图
2.3 微带到SIW的过渡
为了便于和其他微波毫米波电路连接,需要设计微带到介质集成波导的过渡。微带到SIW的过渡结构形式如图3,它的主体为一段微带渐变线,这一段微带渐变线实现介质集成波导和50欧姆微带线之间的阻抗变换。微带渐变线的形式有多种(如圆弧渐变线、线性渐变线等)。由于线性渐变线结构设计简单、加工方便,本文选择了线性微带渐变线。在高频仿真软件HFSS中建模,通过调整变量tt和tw可以快速地实现微带到SIW的过渡。

图3 微带到波导的过渡
3 结果
利用HFSS软件建立基于介质集成波导(SIW)三路零相位功率分配/合成器模型,如图4。通过仿真优化,确定参数a=13.5mm, d=0.5mm, p=0.65mm, L1=L4=4.1mm, L2=L3=4mm, L5=3.9mm, g1=g3= 11.3mm, g2=10mm, tt=6.2mm, tw=3mm。介质采用Rogers5880,介电常数 =2.2,介质厚度h=0.254mm, 50欧姆微带线线宽w= 0.76 mm。仿真结果如图5、6所示。
=2.2,介质厚度h=0.254mm, 50欧姆微带线线宽w= 0.76 mm。仿真结果如图5、6所示。
由图5可以看到,在频率范围为11~12GHz时,输入端 ,隔离度优于
,隔离度优于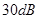 ,三路输出功率分配
,三路输出功率分配 ,不平衡度小于0.3dB。由图6可以看到,在频率范围为11~12GHz时,三路输出
,不平衡度小于0.3dB。由图6可以看到,在频率范围为11~12GHz时,三路输出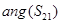 、
、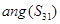 和
和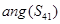 之间的相位差小于6°。
之间的相位差小于6°。

图4 三路零相位功率分配/合成器HFSS模型
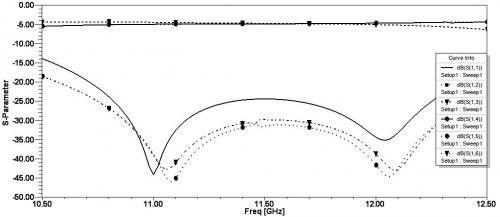
图5 S参数结果

图6 三路相位输出结果
4 结论
本文采用基于SIW的三路零相位功率分配/合成器输入回波损耗好,隔离度高,三路功率等分,不平衡度和相位差都很小,整体尺寸小,性能优良,具有重要的研究和实用价值。
- 基片集成波导多层转换器的设计(08-20)
- 结合基片集成波导和波纹喇叭的混合式单脉冲馈源(04-08)
- 新型Gysel功率分配/合成器的设计(06-12)
- 一种新型四路毫米波空间功率合成技术(11-04)
- 325-500GHz矢量网络分析仪频率扩展系统(06-29)
