高频率稳定性的小型化频率选择表面
1 引言
频率选择表面(Frequency Selective Surface,简称FSS)是一种二维的无限大周期阵列。FSS的单元分贴片型和孔径型两种情况,它们对入射电磁波分别呈现全反射或全透射特性,可以看作是一种对入射角、极化方式、频率等均有作用的空间滤波器。作为一种空间滤波器,FSS在微波和光学领域得到了广泛的应用。FSS可以用作反射面天线的副反射器实现反射面天线系统的频率复用,作为天线覆盖层增加微带天线的增益,也可应用到雷达罩上实现飞行器雷达设备的隐身。
理论上FSS是无限大的周期结构,但在实际应用中FSS都是有限的周期阵列。FSS的无限大周期被截断后,必然会对FSS的性能带来显著的影响。为了保持其原有的特性,通常情况下有限FSS的单元数目不能少于20×20。当实际工作频率很低(如2~4GHz)的时候,FSS单元太大,在实用尺寸之内很难用有限的单元数来体现FSS的频率选择性。因此FSS的小型化在低频应用时显得尤为重要。目前人们在FSS小型化方面已经做了很多探索,本文设计了一种新型的小型化FSS单元,并对其入射角的频率稳定性进行了分析。与前人的研究成果相比本文设计的小型化FSS单元尺寸更小,有更好的选择性和角度稳定性。
2 FSS小型化单元的设计
根据MUNK理论对于方环单元,当环的周长约为入射波长整数倍时发生谐振。因此可以在原来方环单元的内部空间中弯曲方环边长增加谐振长度就可以在降低中心频率的同时而不增大单元的面积。图1为设计的小型化FSS单元的几何结构示意图。其中Dx,Dy为FSS的周期,它们的取值可以相等 也可以不相等,但所取数值必须满足频率选择表面对阵列间距的要求以避免栅瓣的出现。L1和L2分别为方环孔径的内外边长,L3~L7为向内弯曲的各个枝节的长度。图中枝节的长度各不相同,从单元的中心向两边呈阶梯状排列。这样设计的目的旨在最大限度地利用方环的内部空间。W为孔径的宽度,为了能够插入更多的枝节W的取值应尽量小,但所取数值也不能太小,否则电磁波将不再沿着弯曲孔径传播。
图1右边所示为该小型化FSS单元右上角的局部视图。取L1=7.8mm,W=0.2mm,各枝节长度为[L3,L4,L5,L6,L7]=[L2/2.3,L2/2.5, L2/3,L2/5,4*W],其中L2=L1-2×W。单元间距Dx=Dy=8mm,阵列采用正方形栅格排列。介质厚度为1mm,介电常数为2.65。图2是该小型化FSS在电磁波垂直入射时的频率响应。从图中可以看出该小型化单元FSS的中心频率为2.9GHz,-3dB工作带宽为2.62GHz~3.14GHz。在实际应用中可以通过改变枝节的长度来获得需要的工作频率。
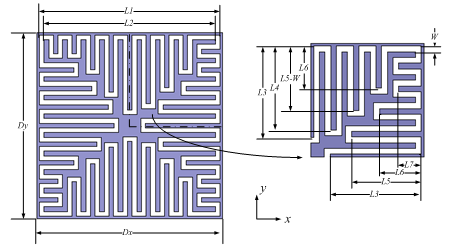
图1 FSS小型化单元结构示意图

图2 小型化FSS的频率响应
该小型化单元和原来的方环单元的尺寸对比如表1所示。从表中可以看出谐振频率都为2.9GHz时,原来方环单元的面积为289mm2,小型化单元的面积仅为64mm2,比原来的方环单元面积缩小了78%。正是由于充分利用了方环的内部空间实现了低频FSS的小型化。
表1 小型化单元和方环单元的尺寸比较(2.9GHz, )
)
| 单元类型 | 谐振频率/GHz | 单元周期/mm | 孔径宽度/mm | 单元面积/mm2 |
| 小型化元 | 2.9 | 8 | 0.2 | 64 |
| 方环单元 | 2.9 | 17 | 0.2 | 289 |
3 小型化FSS的角度稳定性
在实际工程应用中,尤其在雷达天线罩上应用的FSS,绝大多数单元对来波均处于大角度入射状态。因此用于雷达罩上的FSS必须具有很好的角度稳定性,即中心频率不随入射角的增大而改变以保证当入射角很大时雷达通观设备仍然能够正常地工作。对该小型化FSS进行了角度稳定性分析,用软件仿真得到了不同入射角下该小型化FSS的频率响应。如图3所示。
从图3(a)中可以看出对于TM极化,当入射角从0°增大到60°时,该小型化FSS的-3dB工作带宽从1.04GHz减小到530MHz,中心频率几乎没有发生偏移,都谐振在2.9GHz。对于TE极化(图3(b))带宽的变化正好与TM 极化相反,入射角从0°增大到60°时,-3dB工作带宽从1.04GHz增大到1.83GHz,中心频仍然为2.9GHz,几乎不随入射角变化。优异的中心频率稳定性主要取决于单元本身结构的对称性。 60°入射时TE极化响应在5.2GHz处出现了一个较大的栅瓣,这主要是由FSS单元的周期性引起的,对于正方形的栅格排列单元间距D应满
- 随机分布电阻贴片构成的频率选择表面吸波特性研究(11-24)
- 卫星移动通信三大关键技术(07-02)
- 加载Sierpinski垫片天线(01-25)
- 基于LTCC的LNA小型化设计(02-02)
- 复合左右手传输线的带通滤波器小型化设计(06-14)
- 基于Hilbert分形结构的RFID标签天线设计(09-12)
