海底管道检测信标设备水下运动状态研究
时间:06-06
来源:互联网
点击:
2 信标水下运动状态研究
2.1 信标阻力公式的修正
修正球体在介质中沉降速度及介质阻力公式,可以分析计算出信标设备在介质中的沉降规律。球形系数X为相同体积下球体的表面积与非球体的表面积之比,用其表征形状与球体的偏离程度。
经过修正后,非球体在水中所受阻力通式为:
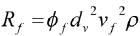
(12)
其中,Φf为非球体在水中所受阻力的阻力系数,dv为体积当量直径,即等体积下球体的直径。vf为非球体在水中的运行速度。非球体在水下的沉降末速公式为:
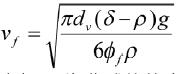
(13)
其中,d为非球体的密度。由公式可知,非球体与流体确定的情况下,
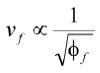
。故沉降末速亦可表示为:
vf=xv0 (14)
v0为等体积球体在水下的沉降末速。
非球体的形状修正系数为:
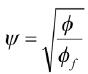
,其值近似等于球形系数,故通常采用该式来计算沉降末速。
一般来说,球体比其他形状的物体更便于介质从周围流过。等体积条件下,球体的表面积最小,球形系数越小,说明物体越不规则,所受的阻力越大,沉降末速也就越小。总信标设备包括压载基座和信标仪器舱。如图3所示。
2.2 信标运动方程的计算
信标下降过程的主要参数如下:
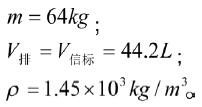
SolidWords计算测得总信标设备的表面积约为:S=1.277m2
计算得出:
体积当量直径:

;
球形系数:
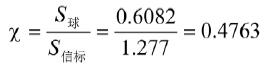
。
修正后的阻力系数为:
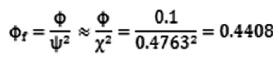
(15)
因
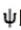
比x略大,取φf=0.4。
修正后的阻力为:
(16)
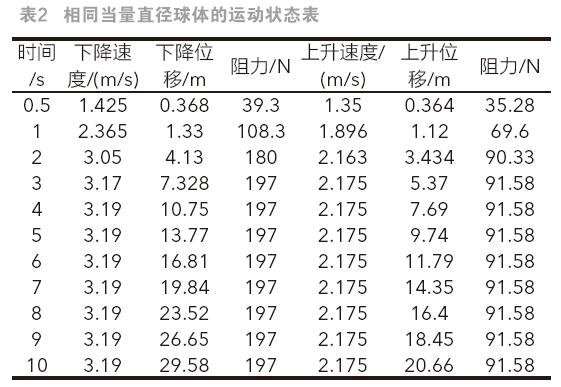
下沉过程中,相同密度和当量直径的球体经过计算后的阻力如下:

(17)
上浮过程中,信标设备的基座留在水下,信标仪器舱解锁上浮,上浮过程的主要参数如下:
SolidWords计算测得信标仪器舱的表面积约为:
s=0.8577m2
计算得出:
体积当量直径:

球形系数:
修正后的阻力系数为:
(18)
因
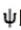
比x略大,取φf=0.25。
修正后的阻力为
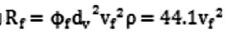
(19)
2.3 MATLAB仿真计算
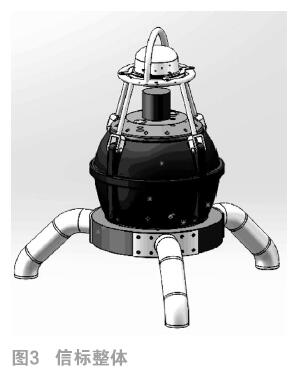
信标下降运动状态仿真如图4;
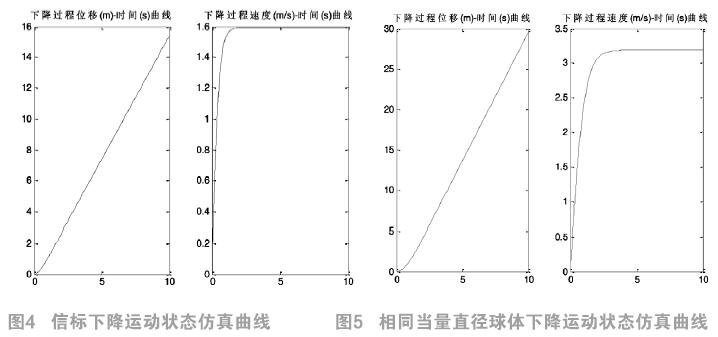
相同当量直径球体下降运动状态仿真曲线如图5;
信标上升运动状态仿真曲线如图6;
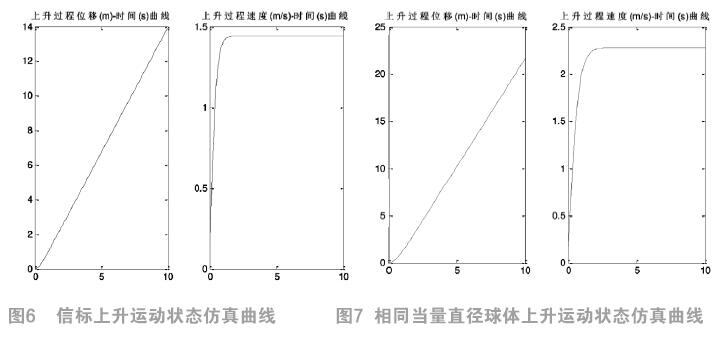
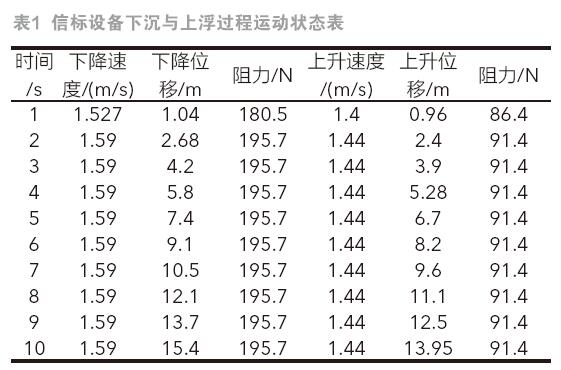
相同当量直径球体上升运动状态仿真曲线如图7。
2.4 信标运动状态结论
信标设备下沉过程中1s达到沉降末速1.59m/s,而后以该速度做匀速直线运动。相同当量直径球体约3s达到沉降末速3.19m/s,后以该速度做匀速直线运动。信标设备上浮过程中1s达到末速1.44m/s,相同当量直径球体约2s达到沉降末速2.175m/s。信标设备的沉降末速约为相同当量直径球体沉降末速的X倍,信标设备的表面积越接近标准球形,其球形系数越接近1,运动末速越接近球体的沉降末速,运动状态越接近具有相同当量直径的球体。可见,该信标的形状与相同当量直径的标准球体相差还是较大的。
3 山东烟台海试
在船上首先将信标连同基座锁紧后投入海里后进行遥控操作,解锁上浮正常。传输距离约为100m,水深约13m ,上浮时间约为8s~9s,平均速度约为1.5m/s。与仿真结果1.44 m/s相差不大。
4 总结
本文通过理论推导和仿真推导海底管道检测信标设备的水下布放与解锁上浮的运动状态,通过海试验证理论推导的正确性,最终验证了李莱曲线和阻力公式应用于信标设备运动分析的正确性和可行性。
参考文献:
[1]杨小平.物理选矿[M].北京:冶金工业出版社,2014:31-35.
[2]朱金波.工程流体力学[M].江苏:中国矿业大学出版社,2008.
[3]孙玉波.重力选矿[M].北京:冶金工业出版社,1982:9-30.
[4]刘卫国.MATLAB程序设计与应用[M].北京:高等教育出版社,2006.
[5]马红旗.鱼雷锚初始贯入海床深度的研究[D].天津大学硕士论文,2010
2.1 信标阻力公式的修正
修正球体在介质中沉降速度及介质阻力公式,可以分析计算出信标设备在介质中的沉降规律。球形系数X为相同体积下球体的表面积与非球体的表面积之比,用其表征形状与球体的偏离程度。
经过修正后,非球体在水中所受阻力通式为:
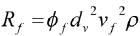
(12)
其中,Φf为非球体在水中所受阻力的阻力系数,dv为体积当量直径,即等体积下球体的直径。vf为非球体在水中的运行速度。非球体在水下的沉降末速公式为:
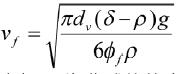
(13)
其中,d为非球体的密度。由公式可知,非球体与流体确定的情况下,
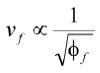
。故沉降末速亦可表示为:
vf=xv0 (14)
v0为等体积球体在水下的沉降末速。
非球体的形状修正系数为:
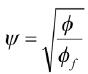
,其值近似等于球形系数,故通常采用该式来计算沉降末速。
一般来说,球体比其他形状的物体更便于介质从周围流过。等体积条件下,球体的表面积最小,球形系数越小,说明物体越不规则,所受的阻力越大,沉降末速也就越小。总信标设备包括压载基座和信标仪器舱。如图3所示。
2.2 信标运动方程的计算
信标下降过程的主要参数如下:
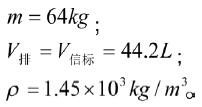
SolidWords计算测得总信标设备的表面积约为:S=1.277m2
计算得出:
体积当量直径:

;
球形系数:
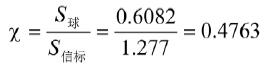
。
修正后的阻力系数为:
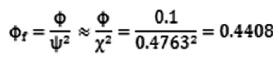
(15)
因
比x略大,取φf=0.4。
修正后的阻力为:
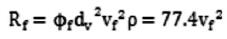
(16)
下沉过程中,相同密度和当量直径的球体经过计算后的阻力如下:

(17)
上浮过程中,信标设备的基座留在水下,信标仪器舱解锁上浮,上浮过程的主要参数如下:
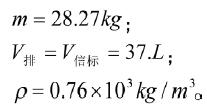
SolidWords计算测得信标仪器舱的表面积约为:
s=0.8577m2
计算得出:
体积当量直径:

球形系数:
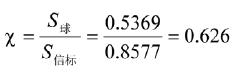
修正后的阻力系数为:
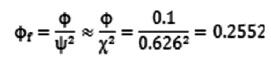
(18)
因
比x略大,取φf=0.25。
修正后的阻力为
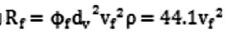
(19)
2.3 MATLAB仿真计算
信标下降运动状态仿真如图4;

相同当量直径球体下降运动状态仿真曲线如图5;

信标上升运动状态仿真曲线如图6;

相同当量直径球体上升运动状态仿真曲线如图7。

2.4 信标运动状态结论
信标设备下沉过程中1s达到沉降末速1.59m/s,而后以该速度做匀速直线运动。相同当量直径球体约3s达到沉降末速3.19m/s,后以该速度做匀速直线运动。信标设备上浮过程中1s达到末速1.44m/s,相同当量直径球体约2s达到沉降末速2.175m/s。信标设备的沉降末速约为相同当量直径球体沉降末速的X倍,信标设备的表面积越接近标准球形,其球形系数越接近1,运动末速越接近球体的沉降末速,运动状态越接近具有相同当量直径的球体。可见,该信标的形状与相同当量直径的标准球体相差还是较大的。

3 山东烟台海试
在船上首先将信标连同基座锁紧后投入海里后进行遥控操作,解锁上浮正常。传输距离约为100m,水深约13m ,上浮时间约为8s~9s,平均速度约为1.5m/s。与仿真结果1.44 m/s相差不大。
4 总结
本文通过理论推导和仿真推导海底管道检测信标设备的水下布放与解锁上浮的运动状态,通过海试验证理论推导的正确性,最终验证了李莱曲线和阻力公式应用于信标设备运动分析的正确性和可行性。
参考文献:
[1]杨小平.物理选矿[M].北京:冶金工业出版社,2014:31-35.
[2]朱金波.工程流体力学[M].江苏:中国矿业大学出版社,2008.
[3]孙玉波.重力选矿[M].北京:冶金工业出版社,1982:9-30.
[4]刘卫国.MATLAB程序设计与应用[M].北京:高等教育出版社,2006.
[5]马红旗.鱼雷锚初始贯入海床深度的研究[D].天津大学硕士论文,2010
- ARM在数字化远程视频监控系统的应用(05-20)
- FPGA在弹上信息处理机中的应用(04-15)
- 与MSP430 USI端口配合使用ADS8361(06-18)
- 基于ARM的I2C设备控制方法的实现(06-11)
- 辰汉电子推出低成本快速量产视频监控方案+4路输入方案(06-24)
- 无线IP视频监控应用即将井喷,Blackfin助您赢得先机(07-23)
